Ομοιόμορφη διακριτή κατανομή
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι έχουμε ένα σύνολο από γεγονότα, όπου το να συμβεί ένα οποιοδήποτε από αυτά είναι εξίσου πιθανό με το να συμβεί ένα οποιοδήποτε άλλο. Τότε λέμε ότι τα γεγονότα αυτά ακολουθούν την ομοιόμορφη κατανομή.
Ακολούθως θα αποκτήσουμε μια εικόνα των παραπάνω με την βοήθεια των ιστογραμμάτων. Συγκεκριμένα, ας υποθέσουμε ότι ρίχνουμε ένα ζάρι κι έχουμε τα εξής 6 ισοπίθανα γεγονότα:
τυχαίνει ⚀,
τυχαίνει ⚁,
τυχαίνει ⚂,
τυχαίνει ⚃,
τυχαίνει ⚄ και
τυχαίνει ⚅.
Οπότε αρχικά εισάγουμε τις ενδείξεις του ζαριού στην R γράφοντας:
Θα εκτελέσουμε 10000 πειράματα και θα δούμε σε αυτά πόσες φορές θα συμβεί το πρώτο γεγονός (⚀), πόσες το 2ο (⚁), πόσες το 3ο (⚂) κτλ. Αυτά τα 10000 πειράματα θα τα κάνουμε 4 φορές και τ’ αποτελέσματά τους θα τα δούμε σε κάποια ιστογράμματα.
Για λόγους αισθητικής και οικονομίας χώρου θα χωρίσουμε την εικόνα σε
4 κομμάτια σαν έναν πίνακα 2×2, οπότε θα χρησιμοποιήσουμε τη συνάρτηση
par(). Συνεπώς γράφουμε:
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(i)
xilies_zaries <- sample(zari, 10000, replace = TRUE)
pin_syxn <- table(xilies_zaries)
barplot(pin_syxn, names.arg = zari)
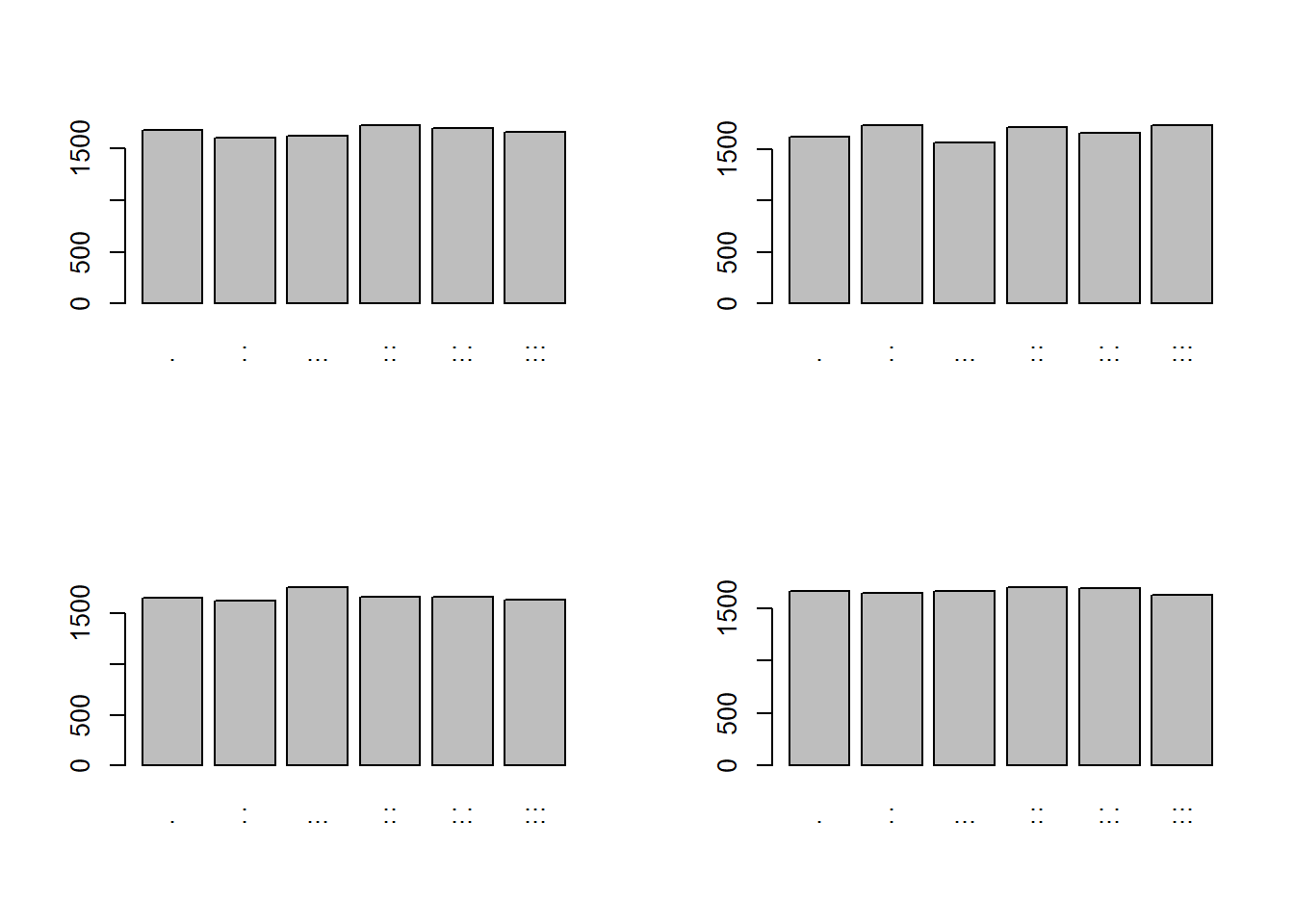
}
Η συνάρτηση set.seed() χρησιμοποιήθηκε ούτως ώστε να
προκύψουν τα ίδια ιστογράμματα και στον αναγνώστη. Ακριβώς επειδή η
επιλογή στοιχείων γίνεται με τυχαίο τρόπο, μπορεί ο αναγνώστης να
τύχαινε σε δείγματα που να του έβγαζαν λιγάκι διαφορετικά ραβδογράμματα.
Αν τώρα θέλει να πειραματιστεί και με άλλα τυχαία δείγματα, πέραν των 4
εικονιζομένων, μπορεί να διαγράψει τη γραμμή 4 με το
set.seed(i).
Τι μας δείχνουν όμως τα ραβδογράμματα αυτά; Τα ραβδογράμματα αυτά δείχνουν τη συχνότητα εμφάνισης του κάθε γεγονότος (⚀, ⚁, ⚂, ⚃, ⚄ και ⚅) και βλέπουμε ότι λίγο-πολύ όλα τα γεγονότα συνέβησαν με την ίδια συχνότητα, τις ίδιες περίπου φορές, πράγμα που αντικατοπτρίζει το γεγονός ότι είχαν την ίδια πιθανότητα (\(=\frac{1}{6}\approx. 0.1666667\approx 16.66\%\)) να συμβούν.
Όλος ο κώδικας παρατίθεται παρακάτω.