Αρνητική διωνυμική κατανομή
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι εκτελούμε ένα τυχαίο πείραμα με δυο πιθανά αποτελέσματα (π.χ. επιτυχία – αποτυχία) κι ενδιαφερόμαστε να έχουμε κάποιον συγκεκριμένο αριθμό επιτυχιών. Το πλήθος των αποτυχιών μέχρι να συμβούν οι επιτυχίες που θέλαμε ακολουθεί την αρνητική διωνυμική κατανομή.
Θα δούμε καλύτερα την κατάσταση με μία προσομοίωση ενός τυχερού παιχνιδιού. Η ευρωπαϊκή ρουλέτα, λοιπόν, έχει 37 νούμερα: 0, 1, 2, 3,… , 37. Από αυτούς τους αριθμούς οι 18 είναι χρωματισμένοι με κόκκινο, άλλοι 18 με μαύρο και ο ένας που περισσεύει (το 0) με πράσινο.
Ποντάρουμε στα κόκκινα κι ενδιαφερόμαστε για το πλήθος των αποτυχιών μέχρι να τύχουμε 3 νίκες. Θα παίξουμε αυτό το παιχνίδι 1000 φορές και θα δούμε σε πόσες εξ αυτών οι 3 νίκες επιτεύχθησαν με τη μία (κάναμε 3 προσπάθειες, είχαμε 0 αποτυχίες), σε πόσες μεσολάβησε 1 αποτυχία (κάναμε 4 προσπάθειες, είχαμε 1 αποτυχία) κτλ.
Γράφουμε λοιπόν:
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(100*i)
xilia_paixnidia <- rnbinom(1000, 3, 18/37)
pin_syxn <- table(xilia_paixnidia)
barplot(pin_syxn)
}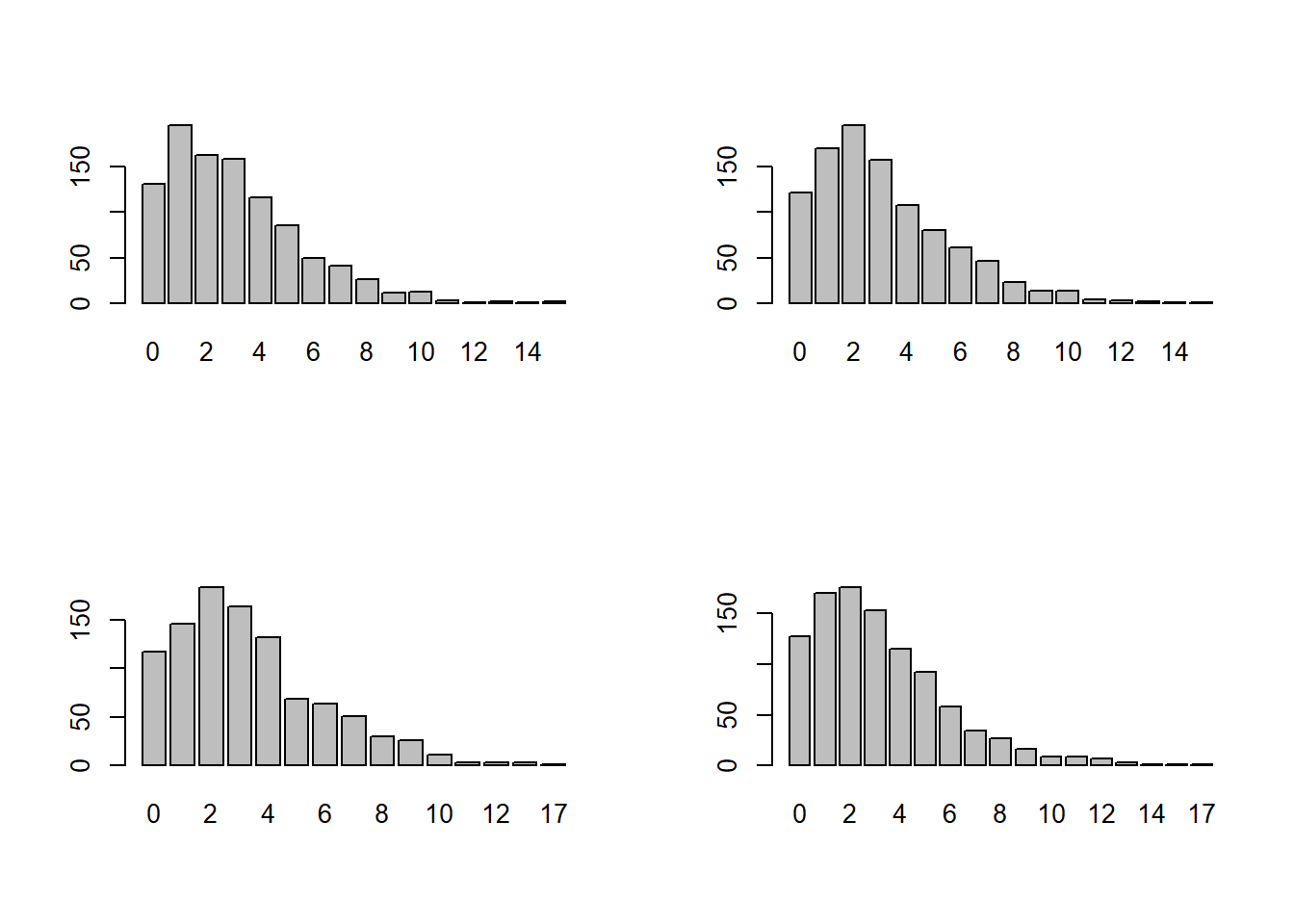
Από τα ραβδογράμματα διαπιστώνουμε ότι ως επί το πλείστον θα χρειαστούν 2 αποτυχημένες προσπάθειες, μέχρι να πετύχουμε 3 νίκες στη ρουλέτα. Επίσης, σπάνια οι 3 νίκες θα καθυστερήσουν τόσο πολύ, ώστε να χρειαστούν 10 οι και περισσότερες αποτυχίες.
Ας δούμε τώρα ποια η πιθανότητα να παίξουμε 10 φορές μέχρι να τύχουμε
την 3η νίκη. Χρειαζόμαστε τη συνάρτηση dnbinom(). Ας
υποθέσουμε ότι εκτελούμε ένα τυχαίο πείραμα με δυο πιθανά αποτελέσματα
(π.χ. επιτυχία – αποτυχία).
Η πιθανότητα επιτυχίας είναι ♠.
Θέλουμε να έχουμε ❌ αποτυχίες,
έως ότου να έχουμε ✅ επιτυχίες σε ανεξάρτητα πειράματα.
Η πιθανότητα να συμβεί αυτό είναι
dnbinom(❌, size = ✅, prob = ♠).
Έτσι, η ζητούμενη πιθανότητα υπολογίζεται από την εντολή:
## [1] 0.03902815από την οποία βρίσκουμε 0.03902815. Έτσι, μπορούμε να είμαστε 3.9% σίγουροι ότι θα έχουμε την 3η νίκη μας μετά από 10 παιχνίδια, δηλαδή μετά από 7 ήττες.
Ολόκληρος ο κώδικας που γράψαμε παρατίθεται παρακάτω: