Κατανομή Poisson
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι ένα γεγονός εμφανίζεται με έναν συγκεκριμένο μέσο ρυθμό σε κάποιο χρονικό διάστημα (ή σε κάποια περιοχή του χώρου). Το πλήθος των εμφανίσεων του γεγονότος αυτού σε αυτό το χρονικό διάστημα (ή σε αυτή την περιοχή του χώρου) ακολουθεί την κατανομή Poisson.
Θα το δούμε καλύτερα με ένα παράδειγμα. Ας υποθέσουμε ότι σε ένα κατάστημα φθάνουν κατά μέσο όρο 8 πελάτες την ώρα. Αυτό δεν σημαίνει, φυσικά, ότι αποκλείεται κάποια συγκεκριμένη ώρα να μην μπει κανένας ή κάποια άλλη να μπουν 20 πελάτες. Λέμε ότι κατά μέσο όρο μπαίνουν 8 πελάτες. Επομένως αξίζει να δούμε πόσο πιθανό είναι να μπουν οι 20 πελάτες που λέγαμε ή να είναι άδειο το μαγαζί για μία ώρα. Το πλήθος των πελατών που εισέρχονται στο κατάστημα σε διάστημα μιας ώρας ακολουθεί την κατανομή Poisson, οπότε θα εξετάσουμε την κατάσταση γράφοντας:
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(100*i)
xilies_ores <- rpois(1000, 8)
pin_syxn <- table(xilies_ores)
barplot(pin_syxn)
}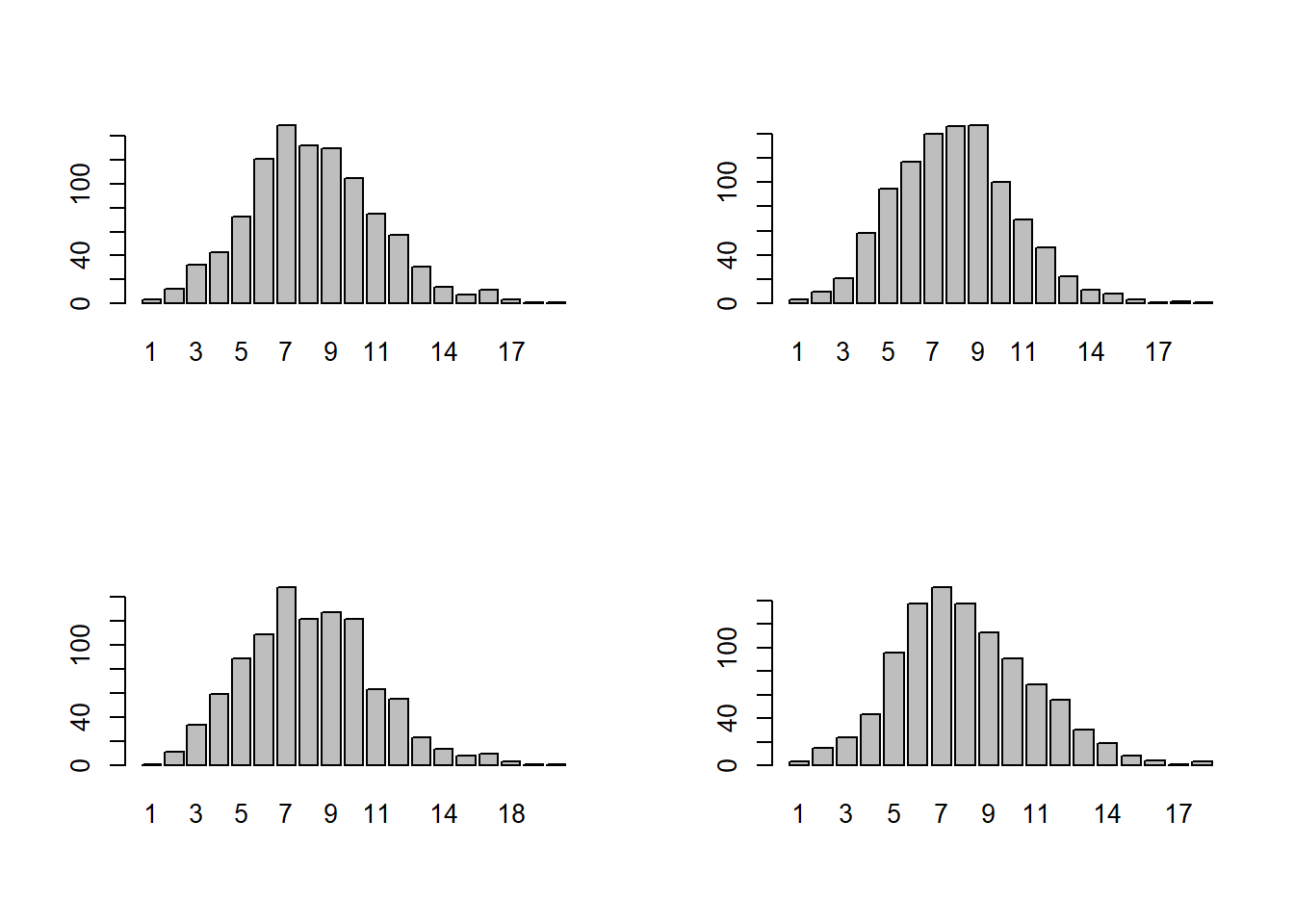
Βλέπουμε κατά συνέπεια ότι συνήθως το μαγαζί μέσα σε μία ώρα θα υποδέχεται 7-9 πελάτες, ενώ σπανίως θα δέχεται πάνω από 15.
Ας πάμε να βρούμε τώρα πόσο πιθανό είναι να μπουν ακριβώς 11 πελάτες
σε μία ώρα. Θα χρειαστούμε τη συνάρτηση dpois(), οπότε θα
γράψουμε:
## [1] 0.07219021Έτσι βρίσκουμε 0.07219021, δηλαδή είναι κατά 7.22% πιθανό να εμφανιστούν ακριβώς 11 πελάτες σε μία ώρα.
Συνολικά ο κώδικάς μας ήταν: