Υπεργεωμετρική κατανομή
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι έχουμε κάποια αντικείμενα, τα οποία χωρίζονται σε δύο κατηγορίες. Συλλέγουμε μια ομάδα εξ αυτών κι ελέγχουμε πόσα αντικείμενα ανήκουν στην μία κατηγορία. Το πλήθος αυτό των αντικειμένων του δείγματος που ανήκουν στην μία κατηγορία ακολουθεί την υπεργεωμετρική κατανομή.
Ας το δούμε πιο συγκεκριμένα. Μία τράπουλα, ως γνωστόν, αποτελείται από 52 φύλλα, εκ των οποίων τα 40 είναι αριθμοί (εδώ θεωρούμε και τους άσσους ως μονάδες) και τα υπόλοιπα 12 φιγούρες.
Παίρνουμε στην τύχη ένα δείγμα 5 χαρτιών και ψάχνουμε να βρούμε πόσα από αυτά είναι φιγούρες. Θα κάνουμε αυτή την τυχαία επιλογή 1000 φορές και θα δούμε σε πόσες έχουμε 5 φιγούρες, σε πόσες 4 φιγούρες, σε πόσες 3, 2 ή 1 φιγούρα και σε πόσες καμία. Αυτή τη 1000άδα επιλογών θα την εκτελέσουμε 4 φορές, ώστε να δούμε ευκρινέστερα τη δράση της τυχαιότητας. Γράφουμε, λοιπόν:
plithos_figoures <- 0:5
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(100*i)
xilia_paixnidia <- rhyper(1000, 12, 40, 5)
pin_syxn <- table(factor(xilia_paixnidia, levels=plithos_figoures))
barplot(pin_syxn, names.arg = plithos_figoures)
}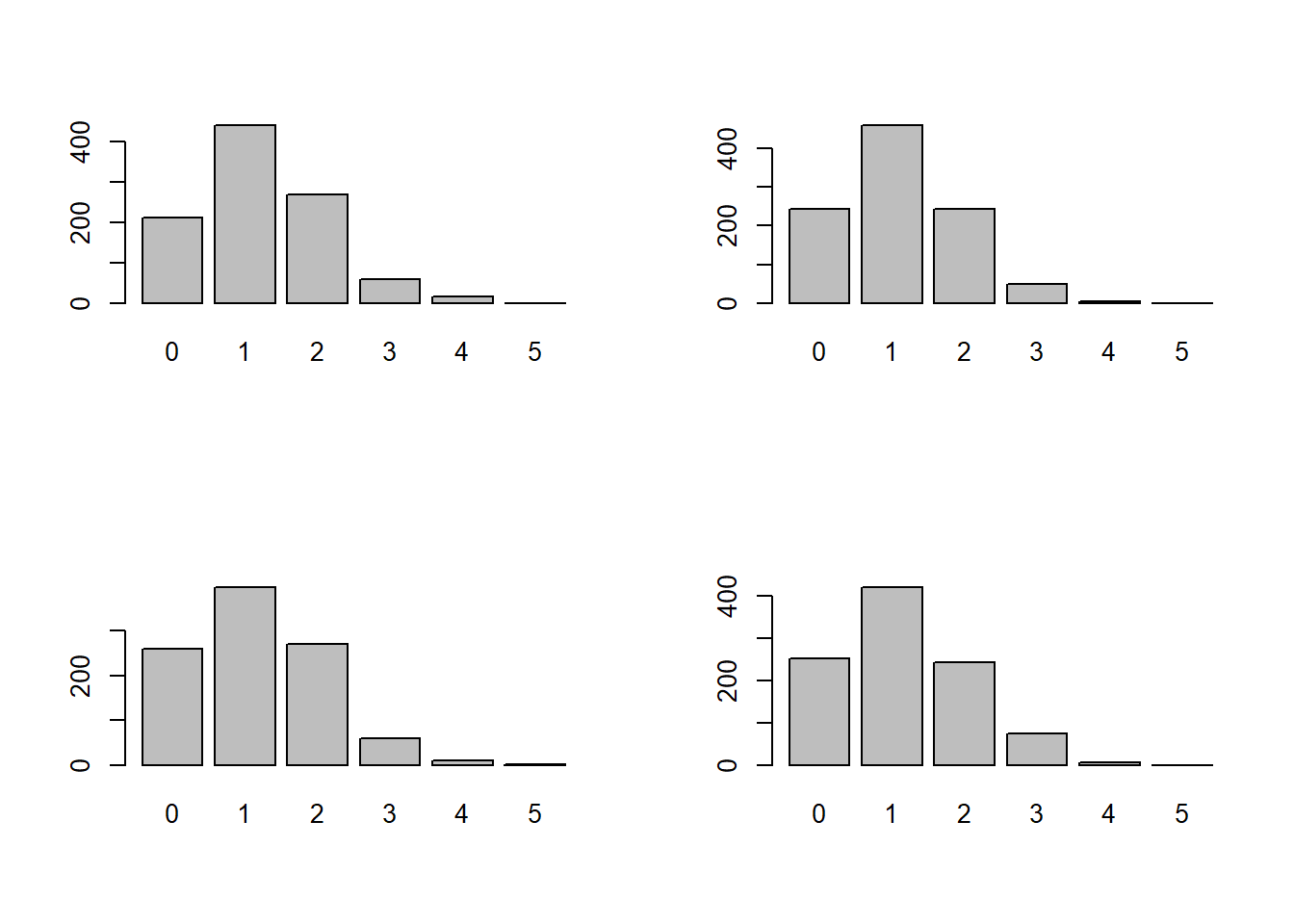
Από αυτά βλέπουμε ότι ως επί το πλείστον θα μας τυχαίνει 1 ακριβώς φιγούρα σε αυτή τη «χεριά» 5 χαρτιών. Σπανίως θα έχουμε 3 ακριβώς φιγούρες και ακόμα σπανιότερα 4 ή 5.
Ας δούμε τώρα πώς μπορούμε να βρούμε ακριβώς τις πιθανότητες αυτών
των ενδεχομένων. Συγκεκριμένα, αν πάρουμε στην τύχη ένα δείγμα 5
χαρτιών, τότε πόση είναι η πιθανότητα τα 3 να είναι φιγούρες και τα 2 να
είναι αριθμοί; Προς τούτο θα χρειαστούμε τη συνάρτηση
dhyper().
Ας υποθέσουμε ότι έχουμε κάποια αντικείμενα:
Από αυτά τα ♂ είναι της κατηγορίας Α και
τα ♀ είναι της κατηγορίας Β.
Από τα αντικείμενα αυτά παίρνουμε ένα δείγμα ❀ αντικειμένων.
Ενδιαφερόμαστε για την πιθανότητα στο δείγμα μας να είναι 🚹 αντικείμενα της κατηγορίας Α.
Αυτή δίνεται από τον τύπο dhyper(🚹, ♂, ♀, ❀). Οπότε,
εμείς εν προκειμένω γράφουμε:
## [1] 0.06602641ή
## [1] 0.06602641Σε κάθε περίπτωση βρίσκουμε πιθανότητα 0.06602641, δηλαδή μπορούμε να είμαστε 6.6% σίγουροι ότι σε ένα «χέρι» 5 χαρτιών θα έχουμε 3 φιγούρες και 2 αριθμούς.
Συνολικά ο κώδικάς μας είναι ο κάτωθι: