Εκθετική κατανομή
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι ένα γεγονός εμφανίζεται με έναν συγκεκριμένο μέσο ρυθμό σε κάποιο χρονικό διάστημα (ή σε κάποια περιοχή του χώρου). Ο χρόνος μεταξύ δύο διαδοχικών εμφανίσεων του γεγονότος αυτού ακολουθεί την εκθετική κατανομή.
Ας επανέλθουμε στο παράδειγμα με την ωριαία πελατεία ενός καταστήματος που είχαμε δει στην ενότητα Κατανομή Poisson. Είπαμε ότι στο κατάστημα μπαίνουν κάθε ώρα κατά μέσο όρο 8 πελάτες ή, με άλλα λόγια, το χρονικό διάστημα από την είσοδο του ενός πελάτη έως του επόμενου είναι κατά μέσο όρο το ⅛ της ώρας. Θέλουμε να μελετήσουμε χρονικό διάστημα θα μεσολαβεί από την είσοδο του ενός μέχρι την είσοδο του άλλου. Είπαμε ότι κατά μέσο όρο είναι το ⅛ της ώρας. Πόσο πιθανό, όμως είναι, να κάνει να μπει κάποιος πελάτης 1 ολόκληρη ώρα ή μισή ώρα; Φυσικά, δεν μας απασχολεί αν κάποιος καθίσει ώρα μέσα στο κατάστημα και μπούνε κι άλλοι κατά τη διάρκεια που είναι αυτός μέσα. Εμείς μετράμε το χρόνο από τη στιγμή που ακούστηκε το «ντιν» στο κουδουνάκι της εισόδου, μέχρι το επόμενο «ντιν».
Θα καταγράψουμε το χρόνο μεταξύ των εισόδων 1000 πελατών κι αυτό θα το κάνουμε 4 φορές. Γράφουμε λοιπόν:
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(100*i)
xilioi_pelates <- rexp(1000, 8)
hist(xilioi_pelates)
}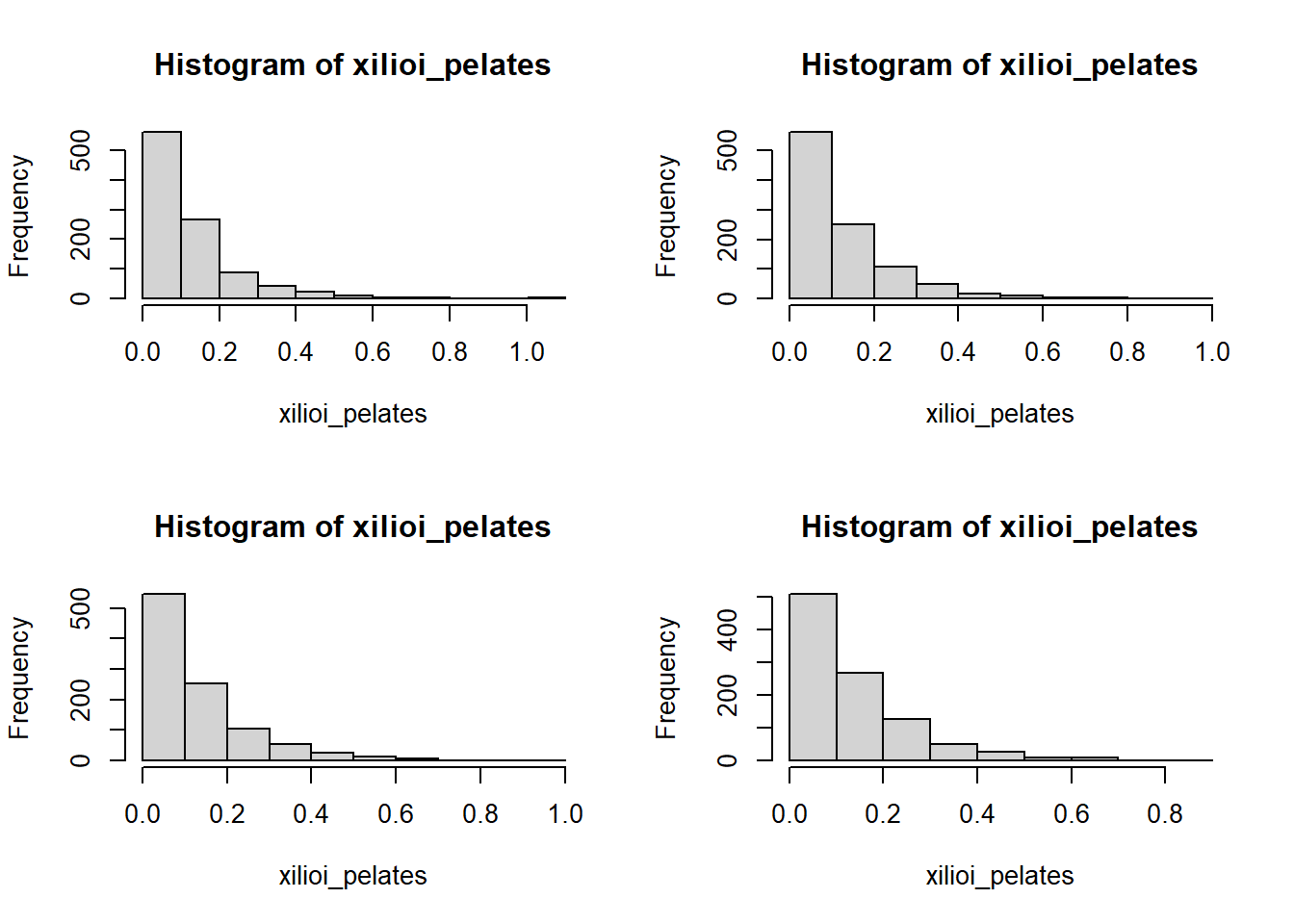
Πάμε τώρα να δούμε τι μας λένε αυτά τα ιστογράμματα. Μας λένε ότι ως επί το πλείστον θα μεσολαβούν από 0 έως 0.1 ώρες (από 0 λεπτά έως 6 λεπτά) από την άφιξη ενός πελάτη, έως και την άφιξη του επόμενου. Είναι, λένε τα ιστογράμματα, σχεδόν απίθανο να μεσολαβήσουν 0.5-0.6 ώρες (30-36 λεπτά) μεταξύ των αφίξεων δύο πελατών.
Ας δούμε όμως τώρα ένα πιο συγκεκριμένο ερώτημα. Πόση είναι η πιθανότητα να μεσολαβήσουν 9 με 15 λεπτά (0.15 με 0.25 ώρες) μεταξύ δύο διαδοχικών αφίξεων; Γράφουμε:
## [1] 0.1658589και βρίσκουμε 0.1658589. Επομένως μπορούμε να είμαστε μόνο κατά 16.59% σίγουροι ότι θα μεσολαβήσουν 9-15 λεπτά μεταξύ των αφίξεων δύο πελατών.
Όλος ο κώδικας που γράψαμε είναι ο κάτωθι: