Διωνυμική κατανομή

Ας υποθέσουμε ότι σε ένα συγκεκριμένο πείραμα κάποιο γεγονός μπορεί να εμφανιστεί ή να; μην εμφανιστεί με κάποια πιθανότητα. Εκτελούμε το πείραμα κάποιες φορές και μετράμε πόσες συνέβη το γεγονός. Οι αριθμοί αυτοί που μπορεί να συνέβη το γεγονός αυτό ακολουθούν τη διωνυμική κατανομή.

Ας το δούμε και πιο συγκεκριμένα. Ρίχνουμε ένα ζάρι 10 φορές κι ενδιαφερόμαστε να δούμε πόσες φορές έχει τύχει ⚅. Ως γνωστόν τα πιθανά ενδεχόμενα είναι τα ⚀, ⚁, ⚂, ⚃, ⚄, ⚅, και αν υποθέσουμε ότι το ζάρι είναι φυσιολογικό, το κάθε ένα τους έχει πιθανότητα \(\frac{1}{6}\). Αναζητούμε, λοιπόν, πόσες φορές θα έχει έρθει ⚅ στις 10 ρίψεις του ζαριού, θεωρώντας ότι ⚅ έρχεται με πιθανότητα \(\frac{1}{6}\). Αυτοί οι αριθμοί, οι φορές που μπορεί να έρθει ⚅ (δηλαδή 1, 2, 3, … , 10 φορές), ακολουθούν τη δυωνυμική κατανομή.

Όπως κάναμε και σε άλλη ενότητα, έτσι κι εδώ θα δούμε τι σημαίνει αυτό με μια προσομοίωση του πειράματος. Αυτή τη φορά θα παίξουμε το παιχνίδια αυτό 1000 φορές και θα δούμε σε πόσα παιχνίδια έτυχε 1 φορά το ⚅ ή 5 φορές ή καμία κτλ. Γράφουμε λοιπόν:

fores <- 0:10
par( mfrow= c(2,2) )
for (i in 1:4) {
  set.seed(100*i)
  xilia_paixnidia <- rbinom(1000, size = 10, prob = 1 / 6)
  pin_syxn <- table(factor(xilia_paixnidia, levels=fores))
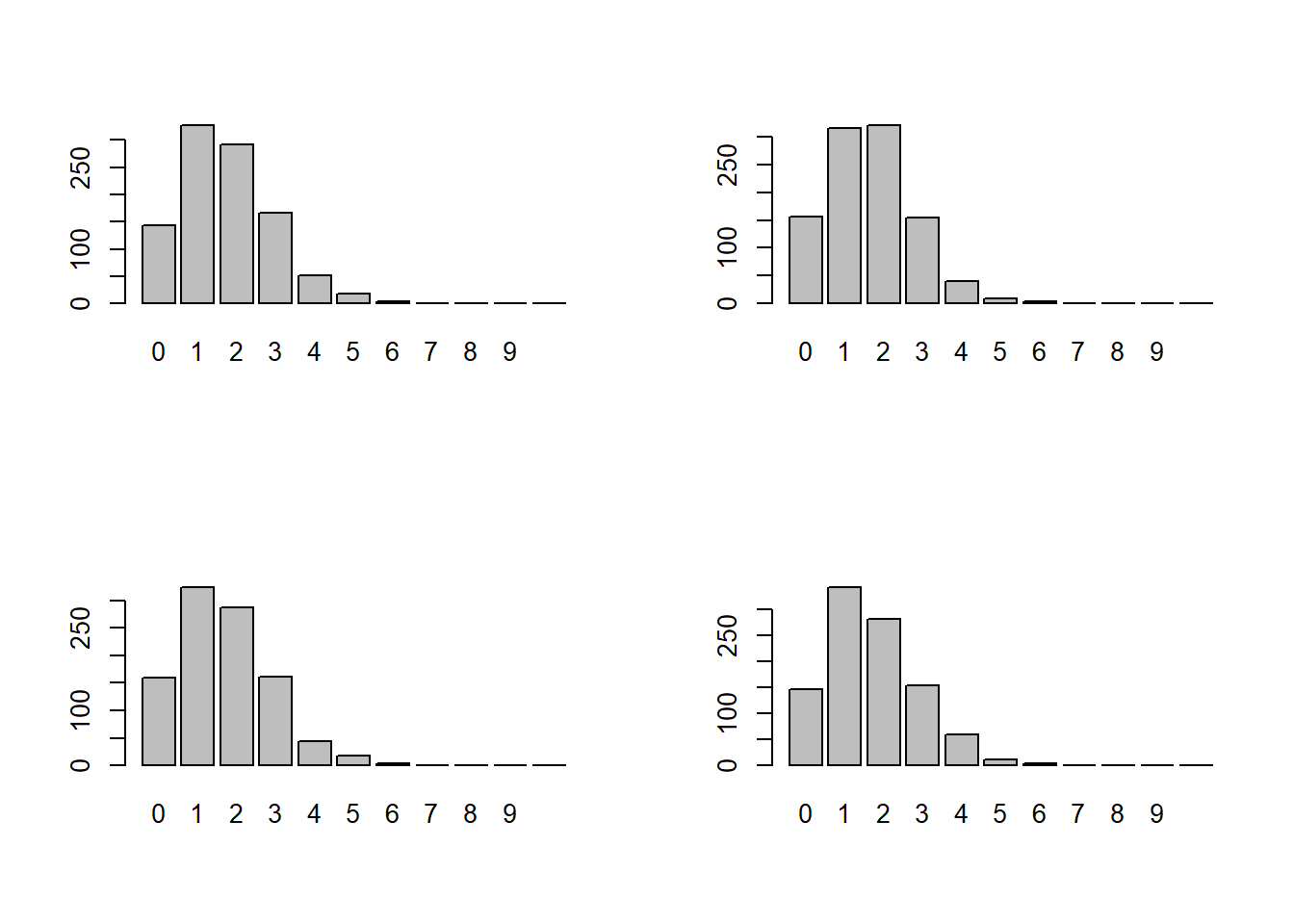
  barplot(pin_syxn, names.arg = fores)
}

όπου η συμπλήρωση table(factor(xilia_paixnidia, levels=fores)), αντί της table(xilia_paixnidia) έγινε διότι κάποιες τιμές δεν συνέβησαν σε κανένα παιχνίδι (πχ δεν έτυχε σε κανένα παιχνίδι να βγαίνει ⚅ 10 φορές, άρα το 10 δεν εμφανίστηκε ποτέ στη λίστα xilia_paixnidia), αλλά εμείς θέλαμε να υπάρχει αυτή η ένδειξη στον οριζόντιο άξονα. Επίσης αυτή τη 1000άδα παιχνιδιών την παίξαμε 4 φορές, ώστε να αποκτηθεί μια καλύτερη εικόνα της τυχαιότητας μέσω των ομοιοτήτων και των διαφορών των ραβδογραμμάτων.

Τι μπορούμε να συμπεράνουμε από αυτά τα ραβδογράμματα; Μπορούμε πχ να συμπεράνουμε ότι σε περίπου 150 παιχνίδια δεν ήρθε ούτε μία φορά ⚅. Επίσης συμπεραίνουμε ότι τις περισσότερες φορές τύχαινε ⚅ μόνο 1 φορά, ενώ είναι εξαιρετικά σπάνιο να τύχει πάνω από 5 φορές ⚅ σε ένα παιχνίδι 10 ρίψεων.

Είδαμε λοιπόν τι σημαίνει η φράση «Οι αριθμοί 0, 1, 2,…, 10 ακολουθούν τη διωνυμική κατανομή \(\mathcal{B}(10,\frac{1}{6})\)». Είδαμε ότι σε αυτή την περίπτωση το να τύχει 3 φορές ⚅ είναι πολύ πιθανότερο απ’ το να τύχει 4. Τι γίνεται όμως αν ενδιαφερόμαστε συγκεκριμένα για την πιθανότητα του ενός και του άλλου ενδεχομένου; Σε αυτό θα μας δώσει απάντηση η συνάρτηση dbinom(). Γράφουμε συνεπώς:

dbinom(3, size=10, prob=1/6)

## [1] 0.1550454

dbinom(4, size=10, prob=1/6) 

## [1] 0.05426588

και μας εξάγονται τα αποτελέσματα 0.1550454 και 0.05426588, αντίστοιχα. Αυτό σημαίνει ότι μπορούμε να είμαστε κατά 15.5% σίγουροι ότι θα τύχει 3 φορές ⚅ σε ένα παιχνίδι 10 ρίψεων, ενώ είμαστε μόνο 5.4% σίγουροι ότι θα τύχει 4 φορές. Αυτήν ακριβώς την διαφορά στις πιθανότητες την περιμέναμε και από τη συζήτηση που κάναμε πάνω στα ραβδογράμματα.

Συνολικά ο κώδικας που γράψαμε είναι ο:

fores <- 0:10
par( mfrow= c(2,2) )
for (i in 1:4) {
  set.seed(100*i)
  xilia_paixnidia <- rbinom(1000, size = 10, prob = 1 / 6)
  pin_syxn <- table(factor(xilia_paixnidia, levels=fores))
  barplot(pin_syxn, names.arg = fores)
}
dbinom(3, size=10, prob=1/6)
dbinom(4, size=10, prob=1/6)