Κατανομή Γάμμα
Κώστας Κούδας
2026-01-27
Ας υποθέσουμε ότι ένα γεγονός εμφανίζεται με έναν συγκεκριμένο μέσο ρυθμό σε κάποιο χρονικό διάστημα (ή σε κάποια περιοχή του χώρου). Ο χρόνος μεταξύ κάποιον αριθμό εμφανίσεων του γεγονότος αυτού ακολουθεί την κατανομή Γάμμα.
Η κατανομή Γάμμα είναι μια γενικευση της εκθετικής κατανομής, αφού η εκθετική κατανομή εξετάζει τον χρόνο ανάμεσα σε δύο διαδοχικές εμφανίσεις ενός γεγονότος, ενώ η κατανομή Γάμμα τον χρόνο ανάμεσα σε ένα οποιοδήποτε πλήθος εμφανίσεων. Αλλά ας το δούμε καλύτερα με ένα παράδειγμα.
Ας υποθέσουμε ότι βρισκόμαστε στο ταχυδρομείο στις 9πμ, παίρνουμε το νούμερο 124 και περιμένουμε τη σειρά μας. Θα θέλαμε να δούμε τον χρόνο που μέλλει να περιμένουμε, οπότε και κοιτάζουμε τι νούμερο εξυπηρετείται εκείνη τη στιγμή. Αυτό είναι το 120. Μας υπολείπονται, λοιπόν, 4 νούμερα, μέχρι να μας φωνάξουν. Ακούγεται λίγο, αλλά μπορεί και να μην είναι. Αυτό εξαρτάται από το πόσο γρήγορα εξυπηρετούνται οι πελάτες. Ρωτάμε, συνεπώς, έναν υπάλληλο «Τι ώρα άνοιξε το ταχυδρομείο για το κοινό;» και μάς απαντά «Στις 8πμ». Οπότε καταλαβαίνουμε ότι σε 60 λεπτά (8πμ έως 9πμ) εξυπηρετήθηκαν 120 νούμερα, ήτοι κατά μέσο όρο 2 πελάτες το κάθε λεπτό. Ή, με άλλα λόγια, εξυπηρετούταν 1 πελάτης κάθε ½ λεπτό.
Εμείς πρέπει να περιμένουμε 4 νούμερα, άρα θα περιμένουμε κατά μέσο όρο 4·½=2 λεπτά. Αυτό όμως κατά μέσο όρο. Μπορεί τελικά να περιμένουμε 10 λεπτά ή και 1 λεπτό. Θα θέλαμε να ξέρουμε πόσο πιθανό είναι το ένα σενάριο και πόσο το άλλο. Για να το βρούμε αυτό θα κάνουμε μια προσομοίωση της εμπειρίας μας στον υπολογιστή. Θα μας βάλουμε να περιμένουμε 1000 φορές αυτά τα 4 νούμερα, υπό τις ίδιες συνθήκες, θα καταγράφουμε τον χρόνο που περιμένουμε κάθε φορά και θα δούμε πόσες φορές περιμέναμε 10 λεπτά, 15 ή κάτι άλλο.
Γράφουμε λοιπόν:
par( mfrow= c(2,2) )
for (i in 1:4) {
set.seed(100*i)
xilioi_pelates <- rgamma(n=1000, shape=4, rate=2)
hist(xilioi_pelates)
}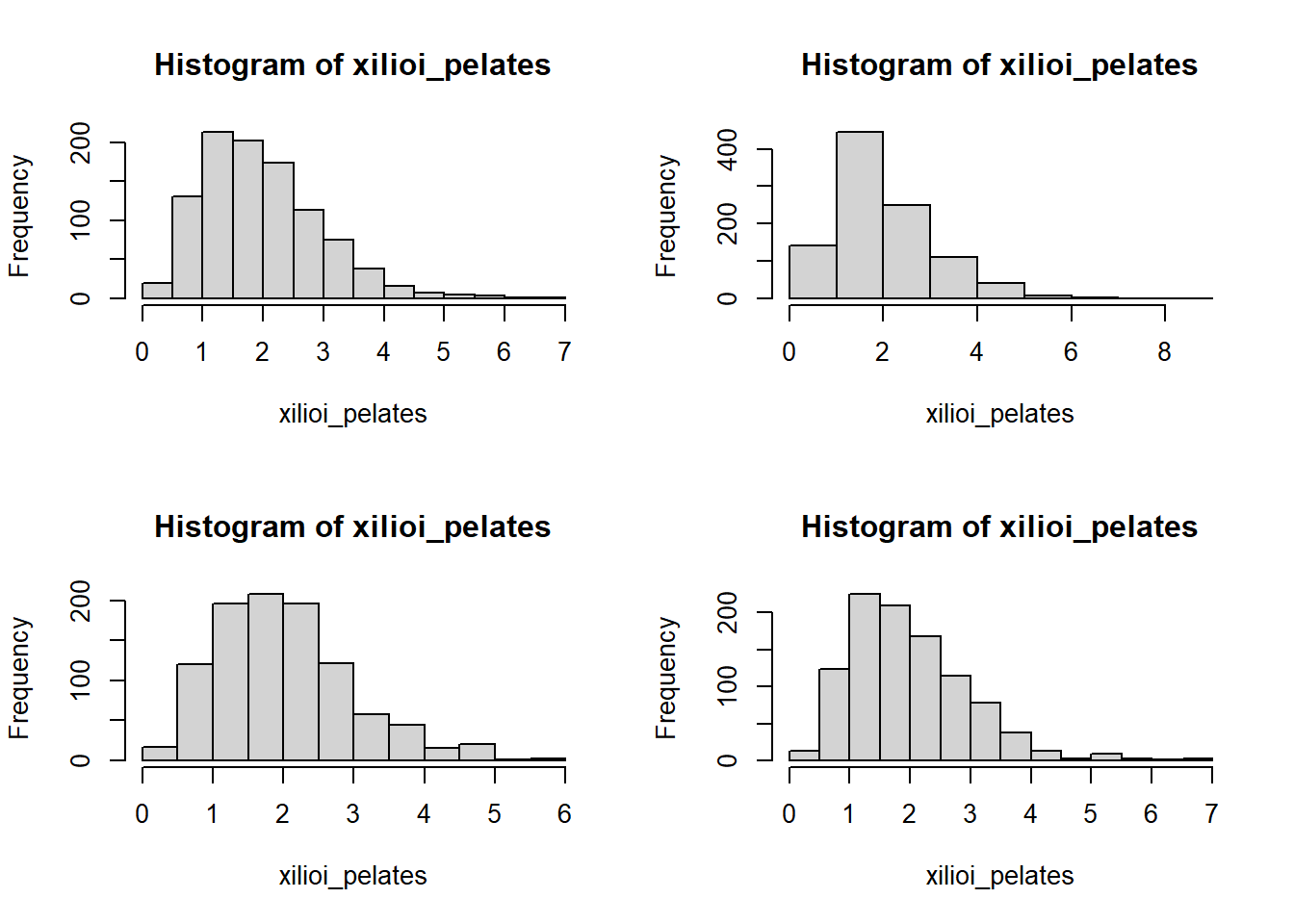
Φυσικά, δεν χρειαζόταν να επαναλάβουμε την 1000άδα προσομοιώσεων 4 φορές, απλά το κάναμε για να έχουμε μια πιο γενική εικόνα της συμπεριφοράς της κατανομής Γάμμα. Αλλά ας δούμε τι διαπιστώνουμε. Από τα παραπάνω ιστογράμματα διαπιστώνουμε ότι ο χρόνος αναμονής μας θα είναι συνήθως περίπου 1 με 2 λεπτά. Από την άλλη, φαίνεται πως δεν είναι απίθανο ούτε το να περιμένουμε λιγότερο από 1 λεπτό, αλλά αρχίζουν και σπανίζουν οι περιπτώσεις όπου εμείς θα χρειαστεί να περιμένουμε πάνω από 3 λεπτά.
Τι γίνεται, όμως, αν μάς ενδιαφέρει η πιθανότητα να περιμένουμε ένα συγκεκριμένο χρονικό διάστημα; Ας υποθέσουμε ότι είμαστε ανυπόμονοι και θα θέλαμε να ξέρουμε πόσο πιθανό είναι να έρθει η σειρά μας σε λιγότερο από 2 λεπτά. Τότε γράφουμε:
## [1] 0.5665299οπότε εξάγεται απάντηση 0.5665299, δηλαδή μπορούμε να είμαστε κατά 57% περίπου σίγουροι ότι θα περιμένουμε λιγότερο από 2 λπτά. Τι γίνεται, όμως, αν μας ενδιέφερε να περιμένουμε από 1 έως 2 λεπτά; Τοιαύτη περιπτώσει θα γράψουμε:
## [1] 0.4236533και η απάντηση που θα προκύψει θα είναι 0.4236533. Επομένως μπορούμε να είμαστε περίπου 42% σιγουροι ότι θα περιμένουμε από 1 έως 2 λεπτά. Τέλος, θα εξετάσουμε την περίπτωση να περιμένουμε πάνω από 5 λεπτά. Ας υποθέσουμε, βρε αδερφέ, ότι θέλουμε να πάρουμε ένα καφεδάκι. Προλαβαίνουμε; Γράφοντας:
## [1] 0.01033605βρίσκουμε ως απάντηση το 0.01033605, άρα μπορούμε να είμαστε μόνο κατά 1% σίγουροι ότι θα κάνει πάνω από 5 λεπτά να έρθει η σειρά μας. Καλύτερα να μην το ρισκάρουμε, λοιπόν.
Ο κώδικας που γράψαμε συνολικά είναι ο κάτωθι: