Διαλέγουμε στην τύχη έναν αριθμό ανάμεσα σε δύο άλλους. Οι αριθμοί αυτοί που διαλέγουμε έτσι ακολουθούν την ομοιόμορφη κατανομή.

Ας υποθέσουμε, για παράδειγμα, ότι η Τροχαία στήνει μπλόκο κάπου σε έναν δρόμο 900 μέτρων. Το μπλόκο μπορεί να είναι οπουδήποτε στον δρόμο αυτό, άρα η θέση του μπορεί να είναι σε οσαδήποτε μέτρα από 0 έως 900 από την αρχή του δρόμου. Με άλλα λόγια, η θέση του είναι κάποια μέτρα στην τύχη στο διάστημα 0 έως 900 από την αρχή του δρόμου. Πόσο πιθανόν είναι, λοιπόν, η αστυνομία να βρίσκεται στη μία ή την άλλη θέση; Θα παρακολουθήσουμε τα μπλόκα αυτά για 1000 μέρες και θα επαναλάβουμε το πείραμα 4 φορές.

Έτσι, γράφουμε:

par( mfrow= c(2,2) )
for (i in 1:4) {
  set.seed(100*i)
  xilies_imeres <- runif(1000, min = 0, max = 900) 
  hist(xilies_imeres)
}

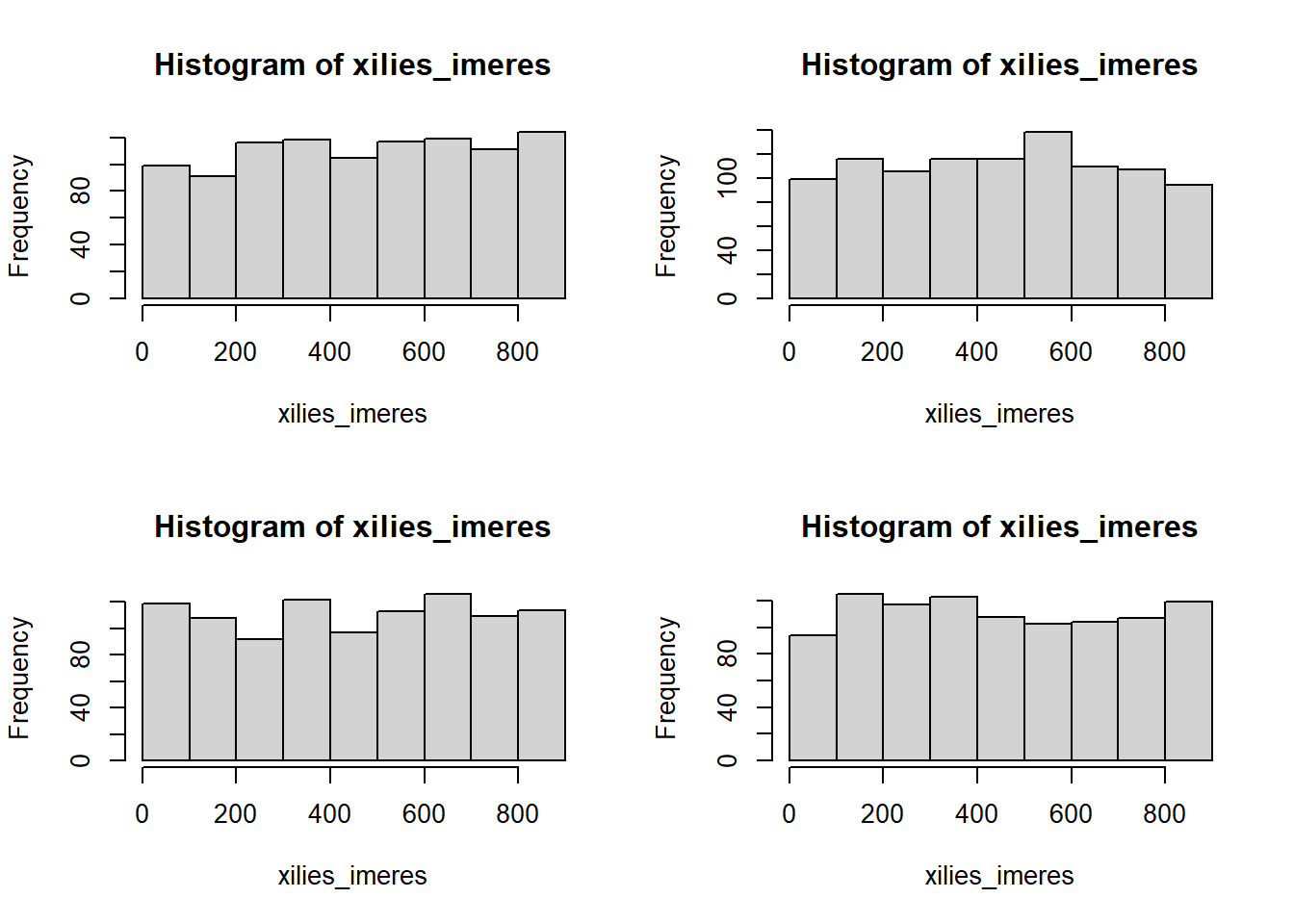
Από αυτά τα ιστογράμματα βλέπουμε ότι δεν έχει εμφανή πιθανότητα παραπάνω να συναντήσει κανείς μπλόκο στα πρώτα 200 μέτρα, έναντι πχ στα επόμενα 200 μέτρα. Το ίδιο συχνά θα δει κανείς μπλόκο πχ στο κεντρικό διάστημα 400 με 500 μέτρα από την αρχή του δρόμου, και το ίδιο λίγο-πολύ συχνά θα δει κανείς μπλόκο σε κάποιο άλλο διάστημα πλάτους 100 μέτρων (για παράδειγμα στο 800-900).

Πόσο όμως είναι η πιθανότητα να τύχουμε μπλόκο στο διάστημα 400-500; Γράφουμε:

punif(500,  min = 0, max = 900)-punif(400,  min = 0, max = 900)
## [1] 0.1111111

Οπότε βρίσκουμε 0.1111111, δηλαδή είμαστε κατά 11.11% σίγουροι ότι θα τύχουμε μπλόκο στο διάστημα αυτό. Στο ίδιο αποτέλεσμα, φυσικά, καταλήγουμε αν πάρουμε οποιοδήποτε άλλο διάστημα πλάτους 100 μέτρων, όπως πχ το 137-237:

punif(237,  min = 0, max = 900)-punif(137,  min = 0, max = 900)
## [1] 0.1111111

Από την άλλη, αν θέλαμε να ξέρουμε κάτι περισσότερο ακριβές, αν θέλαμε επί παραδείγματι το μπλόκο να είναι κάπου ανάμεσα στα 270-280 μέτρα, τότε γράφουμε:

punif(280,  min = 0, max = 900)-punif(270,  min = 0, max = 900)
## [1] 0.01111111

και βρίσκουμε 0.01111111, πράγμα που σημαίνει πολύ μικρότερη σιγουριά (1.11%) για το ότι θα βρίσκεται εκεί η αστυνομία.

Όλος ο κώδικάς μας παρατίθεται πιο κάτω:

par( mfrow= c(2,2) )
for (i in 1:4) {
  set.seed(100*i)
  xilies_imeres <- runif(1000, min = 0, max = 900) 
  hist(xilies_imeres)
}
punif(500,  min = 0, max = 900)-punif(400,  min = 0, max = 900)
punif(237,  min = 0, max = 900)-punif(137,  min = 0, max = 900)
punif(280,  min = 0, max = 900)-punif(270,  min = 0, max = 900)