Στο παρόν κεφάλαιο θ’ ασχοληθούμε πάλι με τις τουρκικές παραβιάσεις του Εθνικού Εναέριου Χώρου και των Εθνικών Χωρικών Υδάτων, οπότε θα χρησιμοποιήσουμε τους πίνακες enaerParab.xlsx και ydataParab.xlsx, αφού πρώτα διαγράψουμε τα προηγούμενα.

rm(list = ls())
  • ydataParab.xlsx (για τα θαλάσια συμβάντα):
ETOS MHNAS PARAB_EXY
2013 Ir 37
2013 Fe 13
2013 Mr 36
2013 Ar 25
2013 Ma 54
2013 In 28
2013 Il 17
2013 Au 11
2013 Se 16
2013 Ok 25
2013 No 20
2013 De 59
2014 Ir 64
2014 Fe 47
2014 Mr 48
2014 Ar 39
2014 Ma 26
2014 In 5
2014 Il 13
2014 Au 35
2014 Se 26
2014 Ok 29
2014 No 21
2014 De 18
2015 Ir 10
2015 Fe 16
2015 Mr 38
2015 Ar 21
2015 Ma 65
2015 In 9
2015 Il 16
2015 Au 30
2015 Se 21
2015 Ok 22
2015 No 16
2015 De 35
2016 Ir 22
2016 Fe 27
2016 Mr 46
2016 Ar 39
2016 Ma 23
2016 In 22
2016 Il 32
2016 Au 41
2016 Se 23
2016 Ok 50
2016 No 39
2016 De 50
2017 Ir 116
2017 Fe 117
2017 Mr 168
2017 Ar 193
2017 Ma 290
2017 In 135
2017 Il 160
2017 Au 172
2017 Se 142
2017 Ok 189
2017 No 179
2017 De 137
2018 Ir 124
2018 Fe 120
2018 Mr 108
2018 Ar 119
2018 Ma 146
2018 In 92
2018 Il 141
2018 Au 134
2018 Se 122
2018 Ok 143
2018 No 113
2018 De 117
2019 Ir 111
2019 Fe 70
2019 Mr 83
2019 Ar 143
2019 Ma 239
2019 In 151
2019 Il 368
2019 Au 274
2019 Se 265
2019 Ok 187
2019 No 141
2019 De 171
2020 Ir 254
2020 Fe 229
2020 Mr 193
2020 Ar 182
2020 Ma 144
2020 In 115
2020 Il 366
  • και enaerParab.xlsx (για τα εναέρια):
ETOS MHNAS PARAB_KEK PARAB_EEX OPL_SXHM EMPLOKES YPERPT_ETH_ED SYNOLO_AER
2009 Ir 65 106 37 13 7 250
2009 Fe 47 123 34 17 2 259
2009 Mr 92 152 36 26 3 306
2009 Ar 41 160 32 27 7 229
2009 Ma 121 163 35 8 2 281
2009 In 57 146 34 25 7 247
2009 Il 50 217 42 33 12 310
2009 Au 48 225 38 34 4 293
2009 Se 43 103 31 27 1 253
2009 Ok 42 69 25 18 0 204
2009 No 47 108 26 5 2 219
2009 De 50 106 25 4 4 227
2010 Ir 70 107 26 1 0 239
2010 Fe 35 84 28 0 1 220
2010 Mr 52 114 40 1 1 324
2010 Ar 45 77 27 0 0 239
2010 Ma 129 156 30 1 0 266
2010 In 56 97 34 1 0 292
2010 Il 58 128 46 7 4 316
2010 Au 43 87 34 0 0 246
2010 Se 46 105 29 2 1 233
2010 Ok 58 92 23 0 1 215
2010 No 74 98 22 0 4 206
2010 De 63 94 28 0 8 234
2011 Ir 70 104 34 0 1 274
2011 Fe 46 84 33 0 0 265
2011 Mr 41 71 31 0 0 245
2011 Ar 47 81 31 0 0 254
2011 Ma 128 133 22 0 0 232
2011 In 41 74 25 0 0 212
2011 Il 46 81 32 0 0 198
2011 Au 41 86 30 0 0 192
2011 Se 43 89 30 5 0 199
2011 Ok 31 54 14 10 2 127
2011 No 27 42 9 1 1 96
2011 De 59 63 16 0 0 147
2012 Ir 66 84 16 1 1 146
2012 Fe 32 53 10 0 1 81
2012 Mr 93 69 21 0 0 174
2012 Ar 37 50 16 0 0 110
2012 Ma 104 107 19 0 0 194
2012 In 60 58 23 0 0 157
2012 Il 50 43 15 0 0 96
2012 Au 34 37 13 0 0 77
2012 Se 36 35 9 0 0 69
2012 Ok 35 31 9 0 0 75
2012 No 75 49 14 0 1 135
2012 De 45 30 11 0 0 91
2013 Ir 47 63 13 0 0 103
2013 Fe 47 63 9 0 0 88
2013 Mr 88 48 11 0 0 118
2013 Ar 40 45 8 0 1 74
2013 Ma 94 111 14 0 1 119
2013 In 34 31 9 0 0 62
2013 Il 48 56 14 0 2 105
2013 Au 29 34 11 0 1 76
2013 Se 48 45 14 0 3 109
2013 Ok 25 26 7 0 0 65
2013 No 52 69 11 0 2 99
2013 De 25 45 8 0 1 66
2014 Ir 71 239 18 0 2 138
2014 Fe 31 100 8 0 0 68
2014 Mr 47 109 13 0 2 105
2014 Ar 65 233 12 2 0 109
2014 Ma 136 426 14 0 2 156
2014 In 52 196 8 0 0 79
2014 Il 45 119 13 0 1 96
2014 Au 40 173 11 0 0 77
2014 Se 104 249 14 0 1 129
2014 Ok 45 125 11 0 3 88
2014 No 79 118 9 0 0 100
2014 De 86 157 14 6 3 124
2015 Ir 36 63 10 2 2 79
2015 Fe 35 97 11 0 5 84
2015 Mr 59 210 14 5 3 127
2015 Ar 65 173 10 5 2 136
2015 Ma 187 362 25 29 5 276
2015 In 66 167 16 14 1 143
2015 Il 61 153 10 5 10 111
2015 Au 39 83 5 4 0 73
2015 Se 70 135 8 5 1 87
2015 Ok 100 190 12 5 3 118
2015 No 60 75 6 1 0 80
2015 De 48 71 6 5 4 70
2016 Ir 68 83 5 3 2 89
2016 Fe 76 136 9 7 1 101
2016 Mr 69 109 5 4 0 77
2016 Ar 130 267 12 14 24 133
2016 Ma 157 321 11 6 6 159
2016 In 46 131 3 1 4 54
2016 Il 25 34 2 0 2 31
2016 Au 21 39 0 0 0 15
2016 Se 53 88 1 0 4 49
2016 Ok 69 176 7 4 4 78
2016 No 122 126 13 13 2 145
2016 De 66 161 18 16 8 85
2017 Ir 65 133 16 10 5 70
2017 Fe 81 257 26 8 11 83
2017 Mr 47 172 20 10 3 79
2017 Ar 65 254 18 20 3 97
2017 Ma 190 642 30 29 1 201
2017 In 71 202 21 25 5 96
2017 Il 59 187 20 17 4 84
2017 Au 111 346 26 15 2 139
2017 Se 134 343 34 16 0 168
2017 Ok 132 401 28 19 2 143
2017 No 93 212 7 6 3 89
2017 De 55 168 11 1 0 81
2018 Ir 94 353 11 7 1 89
2018 Fe 82 377 9 3 6 90
2018 Mr 70 190 18 9 0 68
2018 Ar 101 280 20 14 5 124
2018 Ma 202 361 16 10 0 239
2018 In 98 385 11 8 11 161
2018 Il 84 271 10 9 0 126
2018 Au 68 276 14 5 2 109
2018 Se 113 273 13 7 0 161
2018 Ok 214 381 25 15 4 236
2018 No 134 233 21 13 0 180
2018 De 141 325 28 28 18 192
2019 Ir 146 338 33 33 7 199
2019 Fe 81 245 17 16 0 124
2019 Mr 135 378 26 21 6 193
2019 Ar 136 281 23 32 5 184
2019 Ma 290 506 44 41 2 327
2019 In 127 663 28 30 10 137
2019 Il 118 355 29 39 6 161
2019 Au 95 341 27 39 11 106
2019 Se 132 413 21 15 3 171
2019 Ok 139 507 32 32 21 180
2019 No 199 342 25 28 9 208
2019 De 185 444 39 57 44 234
2020 Ir 189 597 55 69 62 261
2020 Fe 131 541 41 67 54 172
2020 Mr 181 425 36 30 58 190
2020 Ar 132 507 38 46 81 160
2020 Ma 93 420 27 36 47 120
2020 In 120 459 20 25 36 149
2020 Il 125 558 23 28 20 142
2020 Au 281 457 38 51 6 283

Είδαμε ότι η μέση τιμή των παραβιάσεων, η διάμεσος κτλ είναι αριθμοί ενδεικτικοί του συνόλου των τιμών των παραβιάσεων. Πόσο όμως το αντιπροσωπεύουν; Γράφοντας:

mean(enaerParab$PARAB_EEX)
## [1] 190.3857

βρίσκουμε ότι η μέση τιμή των παραβιάσεων είναι 190.3857143 παραβιάσεις το μήνα. Αν πχ το πλήθος των παραβιάσεων είναι από 180 έως 200 το μήνα, η μέση τιμή που βρήκαμε αντιπροσωπεύει επαρκέστατα καθεμία τιμή. Αν όμως οι τιμές είναι απλωμένες σε ένα πολύ ευρύτερο διάστημα, τότε η τιμή αυτή δεν είναι καθόλου αντιπροσωπευτική.

Εδώ θα εξετάσουμε διάφορους τρόπους με τους οποίους ανακαλύπτουμε πόσο απλωμένες είναι οι τιμές κάποιων παρατηρήσεων.

1 Εύρος

Το πιο απλό μέτρο διασποράς είναι το εύρος.

Εύρος
Το εύρος ενός συνόλου μετρήσεων (δείγματος ή πληθυσμού) είναι η διαφορά της μικρότερης από την μεγαλύτερη τιμή.

Για να βρούμε το εύρος στην R θα χρησιμοποιήσουμε την συνάρτηση range(). Γράφοντας:

range(enaerParab$PARAB_EEX)
## [1]  26 663

εξάγονται οι αριθμοί 26 και 663. Αυτοί είναι οι ανώτερη και η κατώτερη τιμή της λίστας των παραβιάσεων ΕΕΧ. Προφανώς, το εύρος θα είναι 663-26=637.

2 Τυπική απόκλιση

Δυστυχώς, το εύρος είναι αρκετά ευαίσθητο στις ακραίες τιμές. Αν, επί παραδείγματι, σ’ ένα μήνα έγιναν 1000 παραβιάσεις και σ’ έναν άλλο μόνο 1, το εύρος θα πάρει αυτομάτως την τιμή 999, χωρίς όμως αυτή να αντιπροσωπεύει κάτι ουσιαστικό, αφού αυτές οι ακραίες τιμές έγιναν μόνο δύο φορές.

Τυπική απόκλιση
Η τυπική απόκλιση ενός συνόλου τιμών είναι ένα μέτρο της απόστασής τους από τη μέση τιμή τους.

Η τυπική απόκλειση υπολογίζεται διαφορετικά, όταν μιλάμε για πληθυσμό σε σχέση με όταν μιλάμε για δείγμα. Έτσι, η τυπική δειγματική τυπική απόκλιση υπολογίζεται στην R μέσω της συνάρτησης sd(). Οπότε, γράφοντας:

sd(enaerParab$PARAB_EEX)
## [1] 147.9733

βρίσκουμε ότι η τυπική απόκλιση των παραβιάσεων ΕΕΧ είναι 147.9733393 παραβιάσεις.

Όπως αναφέραμε, η R υπολογίζει διαφορετικά την πληθυσμιακή τυπική απόκλιση. Για την ακρίβεια δεν έχει έτοιμη συνάρτηση για τον υπολογισμό της τυπικής απόκλισης πληθυσμού, οπότε πάλι θα χρειαστεί να την φτιάξουμε εμείς. Αυτό θα γίνει με την εντολή:

sdPop <- function(x) sqrt(mean((x-mean(x))^2))

2.1 Απομονωμένα σημεία

Απομονωμένα σημεία
Μια τιμή από ένα σύνολο μετρήσεων (δείγματος ή πληθυσμού), η οποία είναι πολύ μεγάλη ή πολύ μικρή σε σχέση με τις υπόλοιπες ονομάζεται απομονωμένο σημείο.

Η σημασία της τυπικής απόκλισης θα φανεί μέσα από τα απομονωμένα σημεία, μέσω του κάτωθι θεωρήματος.

Οτιδήποτε βρίσκεται σε απόσταση από την μέση τιμή μεγαλύτερη από τρεις τυπικές αποκλίσεις είναι πιθανό παράτυπο σημείο. Σχεδόν όλο το δείγμα (τουλάχιστον το 88.8%) βρίσκεται σε μικρότερη απόσταση από τρεις τυπικές αποκλίσεις.

Όσον αφορά τις παραβιάσεις ΕΕΧ, γράφοντας:

mean(enaerParab$PARAB_EEX)-3*sd(enaerParab$PARAB_EEX)
## [1] -253.5343
mean(enaerParab$PARAB_EEX)+3*sd(enaerParab$PARAB_EEX)
## [1] 634.3057

βρίσκουμε τους αριθμούς -253.5343036 και 634.3057322 που είναι τα άκρα του διαστήματος εκτός του οποίου εντός του οποίου, όπως είπαμε, βρίσκεται τουλάχιστον το 88.8% του δείγματος. Και όντως! Γράφοντας:

enaerParabApon <- enaerParab[enaerParab$PARAB_EEX>634.3057, ]
enaerParabApon
## # A tibble: 2 × 8
##    ETOS MHNAS PARAB_KEK PARAB_EEX OPL_SXHM EMPLOKES YPERPT_ETH_ED SYNOLO_AER
##   <dbl> <chr>     <dbl>     <dbl>    <dbl>    <dbl>         <dbl>      <dbl>
## 1  2017 Ma          190       642       30       29             1        201
## 2  2019 In          127       663       28       30            10        137

βρίσκουμε ότι μόνο σε δύο μήνες (Μάιος 2017 και Ιούνιος 2019) ότι υπήρξαν παραβιάσεις εκτός του διαστήματος (-253.5343036, 634.3057322). Προφανώς δεν έχει αξία να ψάξουμε για τιμές πλήθους παραβιάσεων μικρότερες του -253.5343036.

3 Ενδοτεταρτημοριακό εύρος

Ενίοτε μπορεί να μη μας απασχολεί το εύρος όλων των μετρήσεων που διαθέτουμε, αλλά κάποιων κεντρικών τιμών τους. Το ενδοτεταρτημοριακό εύρος είναι σε αυτά τα πλαίσια και προσδιορίζει το εύρος του κεντρικού 50% των τιμών. Με άλλα λόγια:

Ενδοτεταρτημοριακό εύρος
Το ενδοτεταρτημοριακό εύρος ενός συνόλου μετρήσεων (δείγματος ή πληθυσμού) είναι η διαφορά μεταξύ του 1ου και του 3ου ταταρτημορίου.

Το ενδοτεταρτημοριακό εύρος στην R υπολογίζεται μέσω της συνάρτησης IQR(). Δηλαδή, αν γράψουμε:

IQR(enaerParab$PARAB_EEX)
## [1] 189

παίρνουμε σαν απάντηση την τιμή 189, όπερ σημαίνει ότι οι τιμές του κεντρικού 50% του δείγματος εκτείνονται σ’ ένα διάστημα πλάτους 189 μονάδων. Αυτό μπορούμε να το εξακριβώσουμε γράφοντας επίσης:

quantile(enaerParab$PARAB_EEX)
##    0%   25%   50%   75%  100% 
##  26.0  82.5 133.0 271.5 663.0

οπότε διαπιστώνουμε ότι το κεντρικό 50% του δείγματος είναι μεταξύ των τιμών 82.5 και 271.5, οι οποίες, προφανώς, απέχουν μεταξύ τους 189 μονάδες.

4 Θηκόγραμμα

Με θηκόγραμμα απεικονίζονται τα τεταρτημόρια και τονίζονται τα απομονωμένα σημεία. Αυτό κείτεται παράλληλα με τον άξονα των τιμών της μεταβλητής μας και αποτελείται από:

  • ένα κουτί που αρχίζει από την ένδειξη του 1ου τεταρτημορίου και τελειώνει στην ένδειξη του 3ου,

  • μία γραμμή στη θέση της διαμέσου, η οποία χωρίζει το κουτί σε δύο κομμάτια,

  • δύο γραμμές ως συνέχεια του κουτιού, οι οποίες εκτείνονται έξω από τα όρια του 1ου και του 3ου τεταρτημορίου και καθεμία τους έχει μήκος ενάμιση ενδοτεταρτημοριακό εύρος, εκτός κι αν έχει ξεπεράσει την ανώτατη ή την κατώτατη τιμή (οπότε σταματάει εκεί),

  • τα σημεία έξω από τις προαναφερθείσες γραμμές είναι πιθανά απομονωμένα σημεία κι έχουν ξεχωριστή σήμανση.

Μια εύκολη και γρήγορη κατασκευή ενός θηκογράμματος γίνεται μέσω της συνάρτησης boxplot(). Έτσι, δεν έχουμε παρά να γράψουμε:

boxplot(enaerParab$PARAB_EEX)

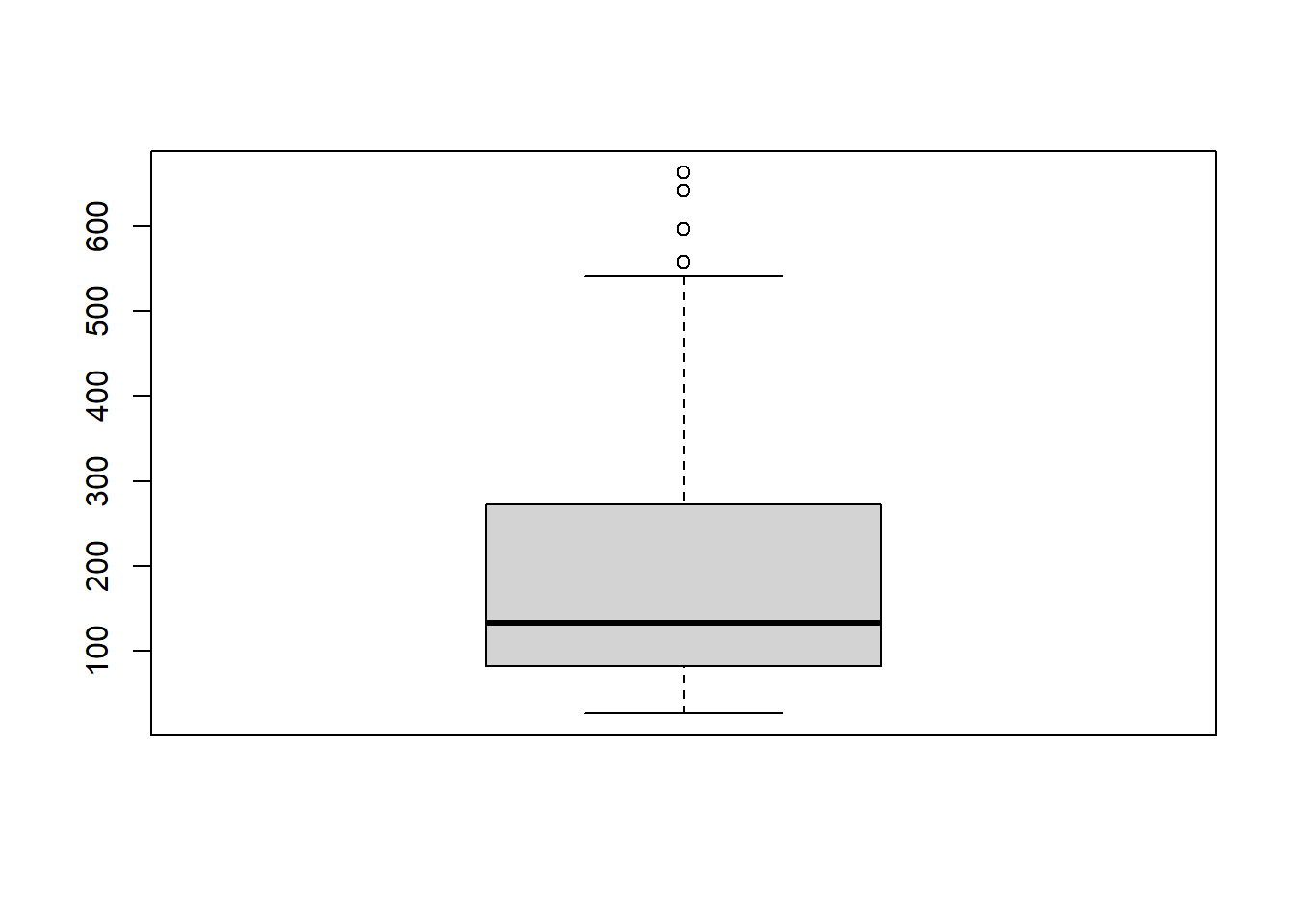
Αν το θέλουμε οριζόντιο, τότε γράφουμε:

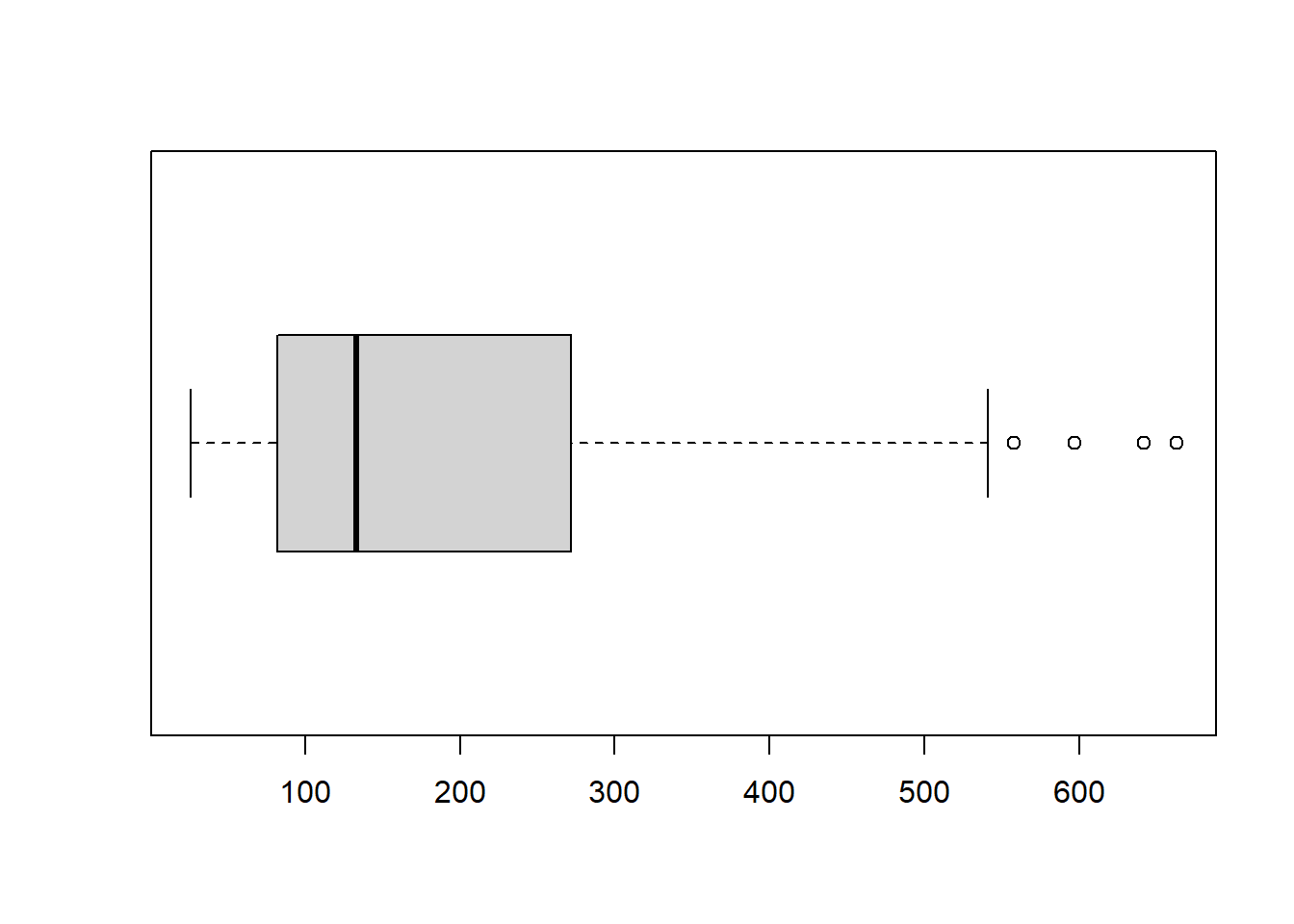
boxplot(enaerParab$PARAB_EEX, horizontal=TRUE)

Για θηκογράμματα με περισσότερη ποικιλία θα απευθυνθούμε στο πακέτο ggplot2, το οποίο επικαλούμαστε μέσω της εντολής library(ggplot2).

Οπότε γράφουμε:

if(!require(ggplot2)){
    install.packages("ggplot2")
    library(ggplot2)
}
ParabEEXbox <- ggplot(enaerParab, aes(x="", y=PARAB_EEX))
ParabEEXbox + geom_boxplot()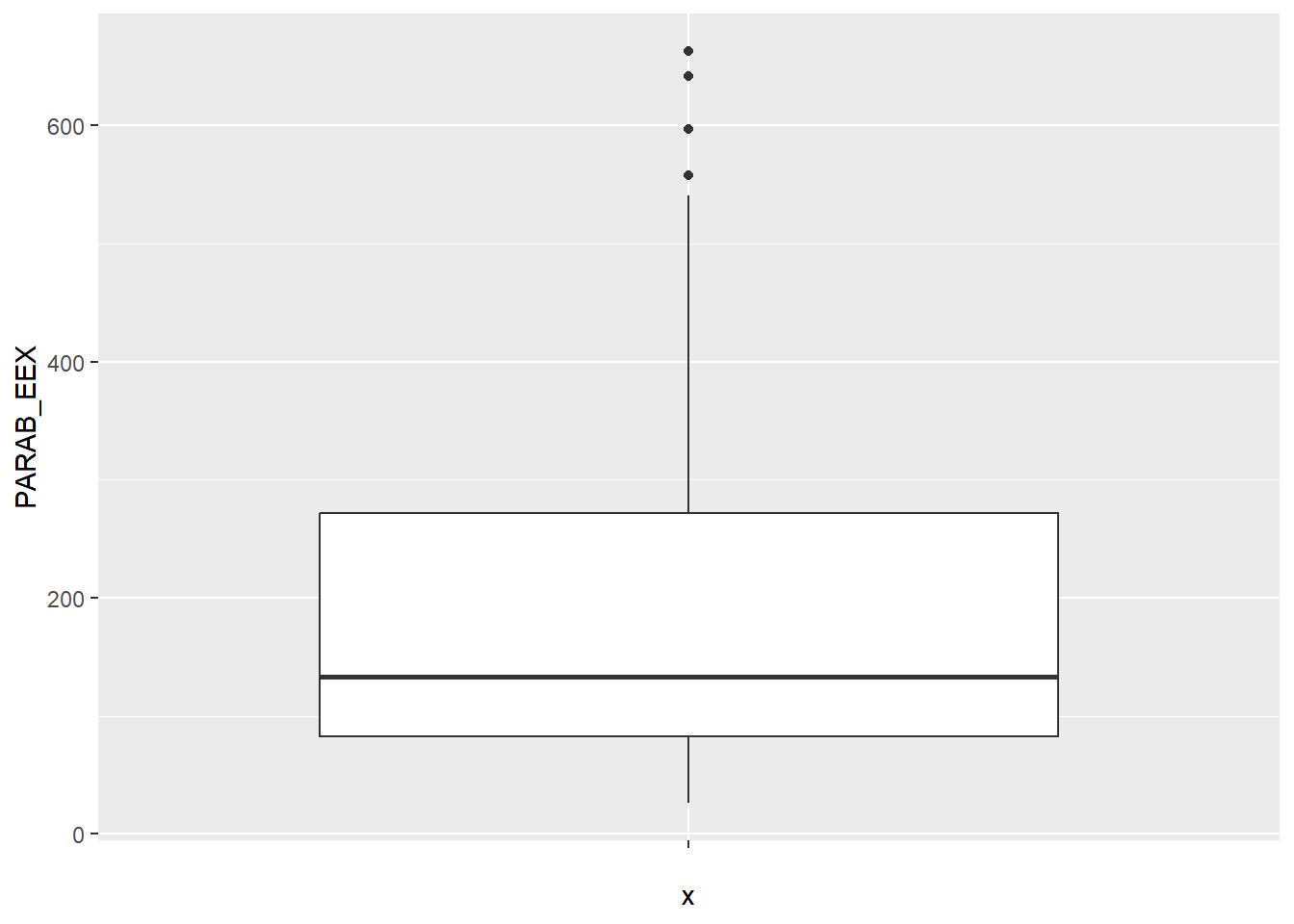

Οπότε έχουμε το θηκόγραμμα που ζητούσαμε. Ο ρόλος της παραμέτρου x="" θα φανεί σε λίγο.

Στην περίπτωση που θελήσουμε το θηκόγραμμα οριζόντιο, δεν έχουμε παρά να γράψουμε:

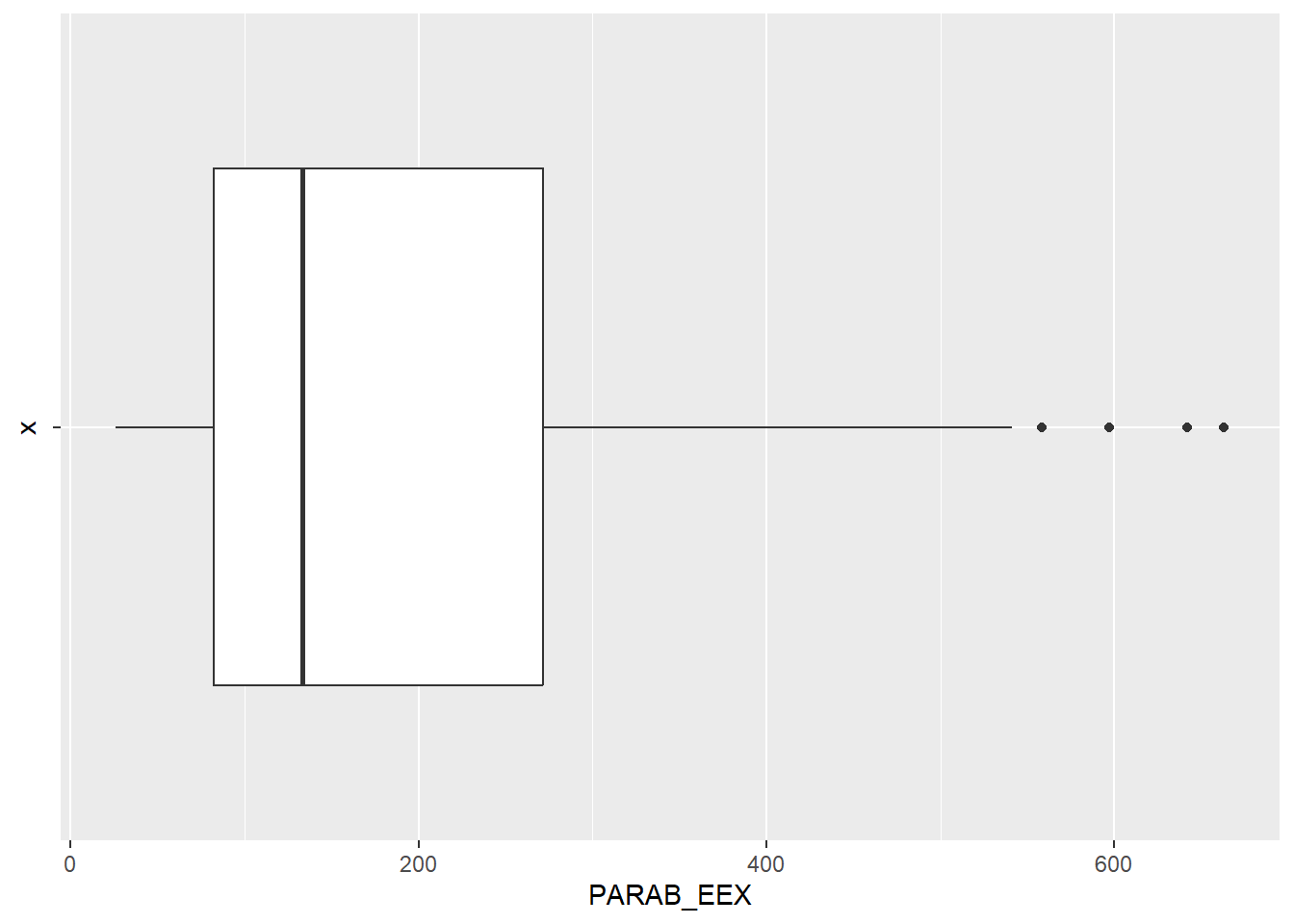
ParabEEXbox + geom_boxplot() + coord_flip()

Δίνοντας κατάλληλες τιμές εντός του geom_boxplot() στα:

  • outlier.shape = και

  • outlier.size =

αλλάξουμε σχήμα και μέγεθος στα απομονωμένα σημεία. Συγκεκριμένα, γράφοντας:

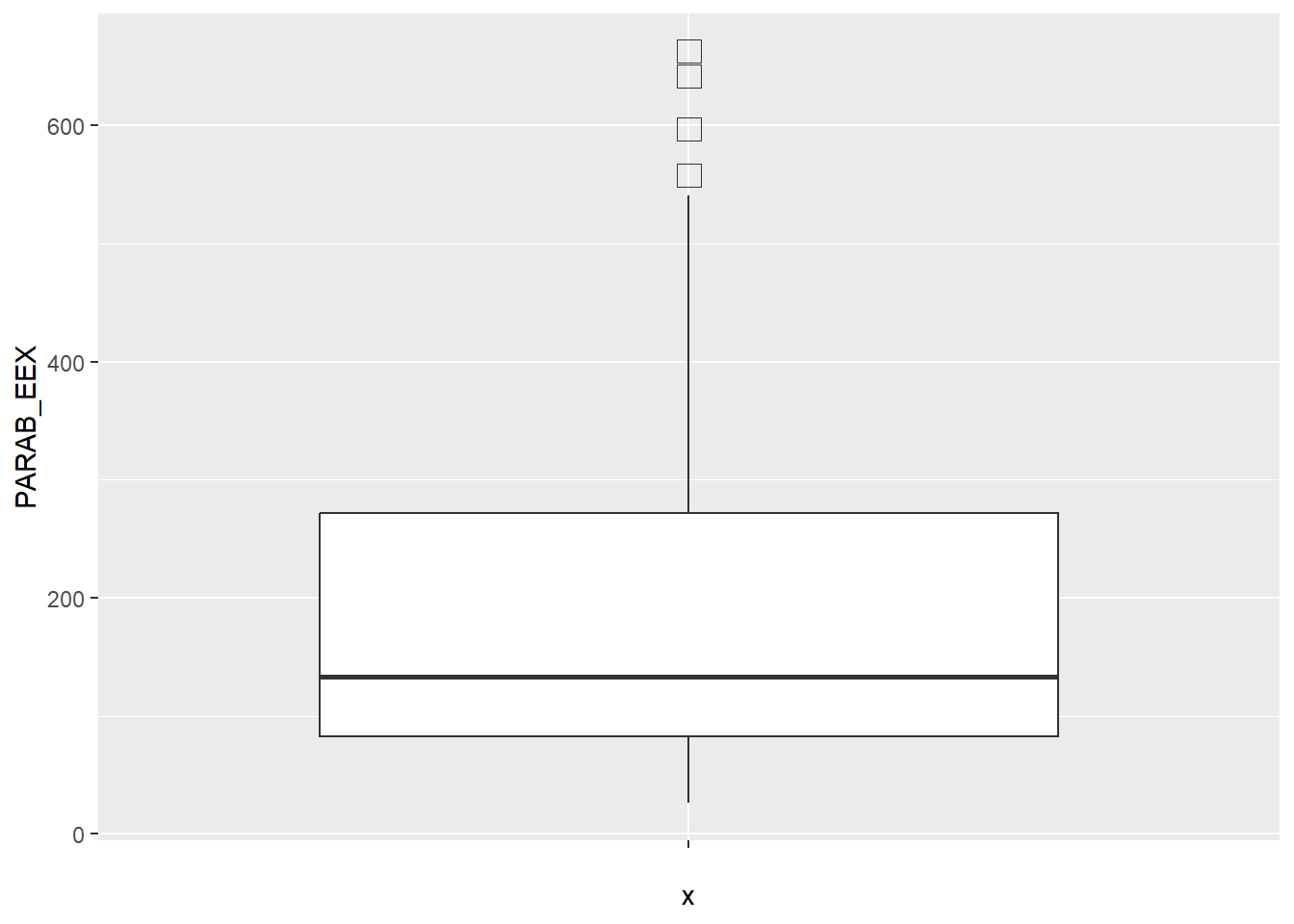
ParabEEXbox + geom_boxplot(outlier.shape = 0, outlier.size = 4)

κάναμε τα απομονωμένα σημεία τετράγωνου σχήματος και πιο μεγάλα.

Ενίοτε μπορεί να θελήσουμε να παραστήσουμε το θηκόγραμμα σε συνδυασμό μ’ ένα σημειόγραμμα. Τοιαύτη περιπτώσει γράφουμε:

ParabEEXbox + geom_boxplot() + geom_dotplot(binaxis='y', stackdir='center', dotsize=1)
## Bin width defaults to 1/30 of the range of the data. Pick better value with `binwidth`.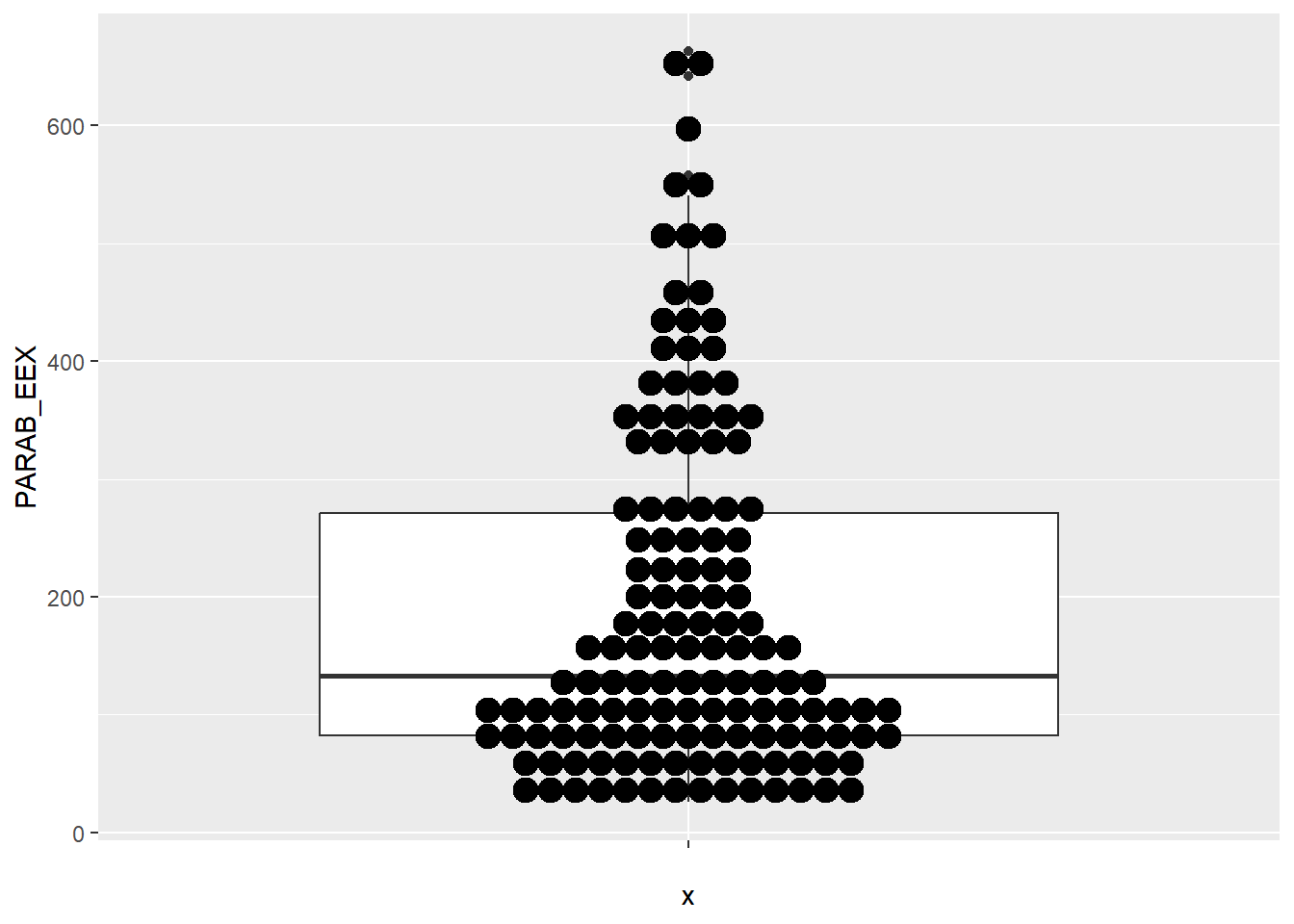

Το σημειόγραμμα θα ήταν πιο ενδιαφέρον, αν τα σημεία του ήταν ατάκτως διατεταγμένα γύρω από τον άξονα συμμετρίας του θηκογράμματος. Αυτό θα επιτευχθεί προσθέτοντας την επιλογή geom_jitter(shape=16, size=1,position=position_jitter(0.2)). Αν όμως γράψουμε κατευθείαν:

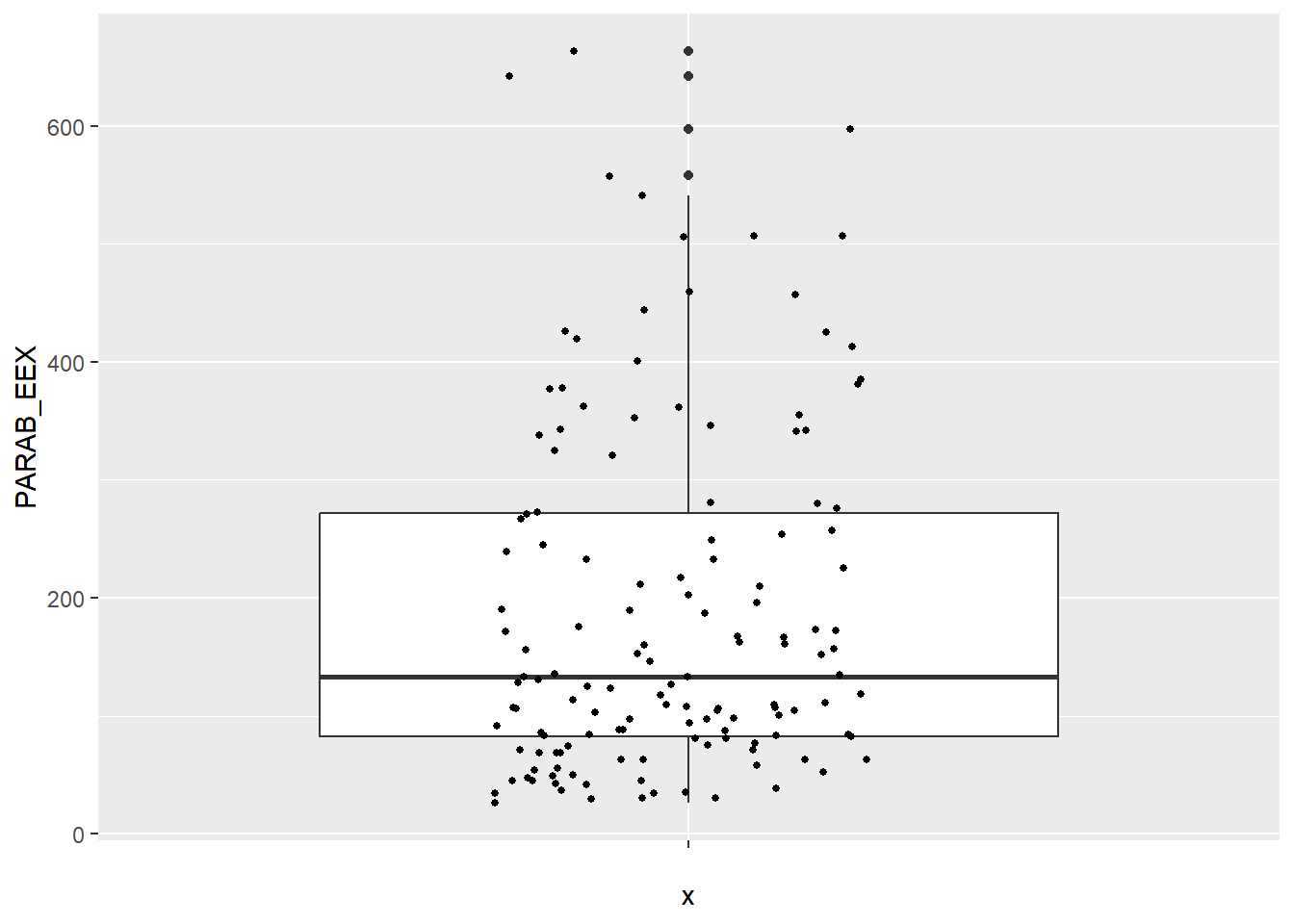
ParabEEXbox + geom_boxplot() + geom_jitter(shape=16, size=1,position=position_jitter(0.2))

θα προκύψουν διπλάσια απομονωμένα σημεία, αφού θα υπάρχουν αυτά από την επιλογή geom_boxplot() και αυτά από τα σημεία που μόλις προσθέσαμε (αυτό μπορεί να γίνει φανερό αλλάζοντας το σχήμα ή το μέγεθος των απομονωμένων σημείων μέσω των επιλογών shape= ή size=).

Οπότε θα πρέπει να σβήσουμε τα απομονωμένα σημεία του θηκογράμματος, πράγμα που θα γίνει είτε μέσω της αλλαγής geom_boxplot(outlier.shape = NA) είτε μέσω της αλλαγής geom_boxplot(outlier.size = -1). Οπότε, για να έχουμε το επιθυμητό θηκόγραμμα, γράφουμε:

ParabEEXbox + geom_boxplot(outlier.shape = NA) + geom_jitter(shape=16, size=1,position=position_jitter(0.2))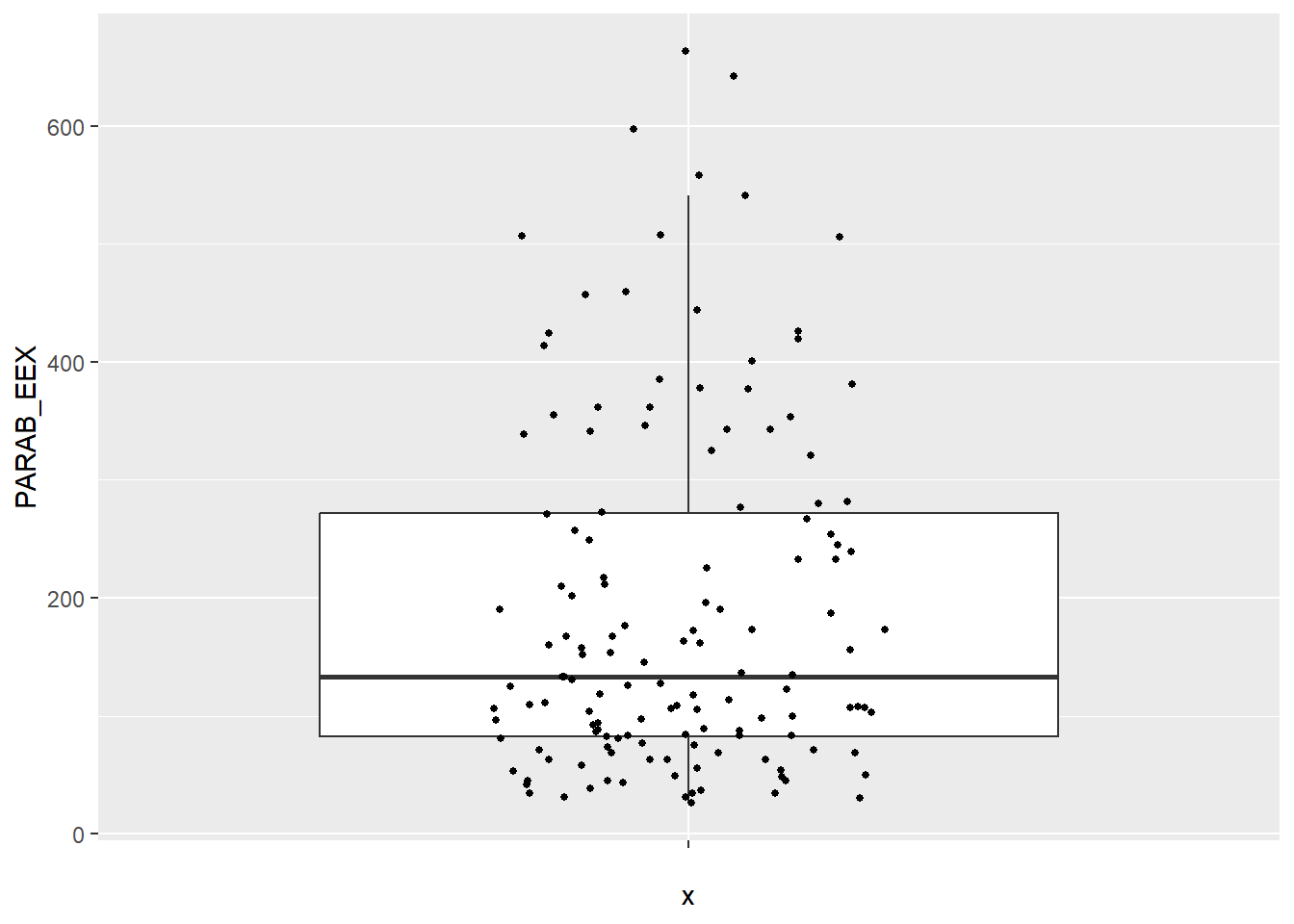

Όσον αφορά την παράμετρο shape= της geom_jitter(), αυτή μας δίνει την επιλογή του σχήματος των σημείων, η size= του μεγέθους και η position= του πόσο απλωμένα θα είναι τα σημεία.

Ας υποθέσουμε τώρα ότι θέλουμε να φτιάξουμε ένα θηκόγραμμα για κάθε έτος ξεχωριστά. Αυτό θα γίνει δίνοντας την οδηγία ο οριζόντιος άξονας (x=) να έχει τα έτη (κι όχι να είναι κενός ενδείξεων, γράφοντας x=""). Αν όμως γράψουμε:

ParabEEXboxEtos <- ggplot(enaerParab, aes(x=ETOS, y=PARAB_EEX))
ParabEEXboxEtos + geom_boxplot()
## Warning: Continuous x aesthetic
## ℹ did you forget `aes(group = ...)`?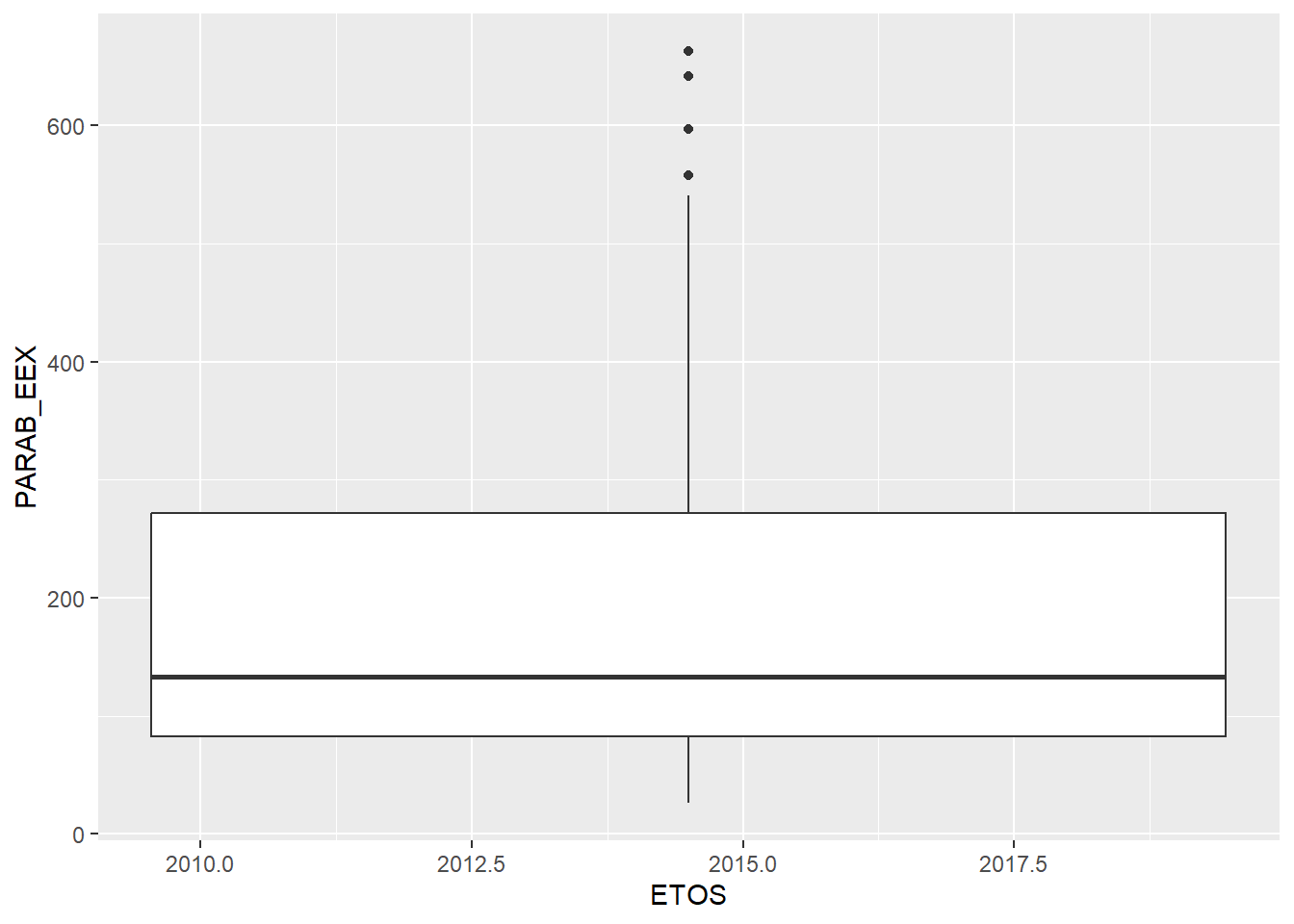

τότε ούτε προκύπτει το επιθυμητό αποτέλεσμα κι έχουμε και μήνυμα σφάλαματος. Αυτό λόγω του ότι οι τιμές της στήλης ETOS είναι αριθμητικές. Θα υπερβούμε αυτό το πρόβλημα μετατρέποντάς τες σε χαρακτήρες, γράφοντας as.character(ETOS), δηλαδή:

ParabEEXboxEtos <- ggplot(enaerParab, aes(x=as.character(ETOS), y=PARAB_EEX))
ParabEEXboxEtos + geom_boxplot()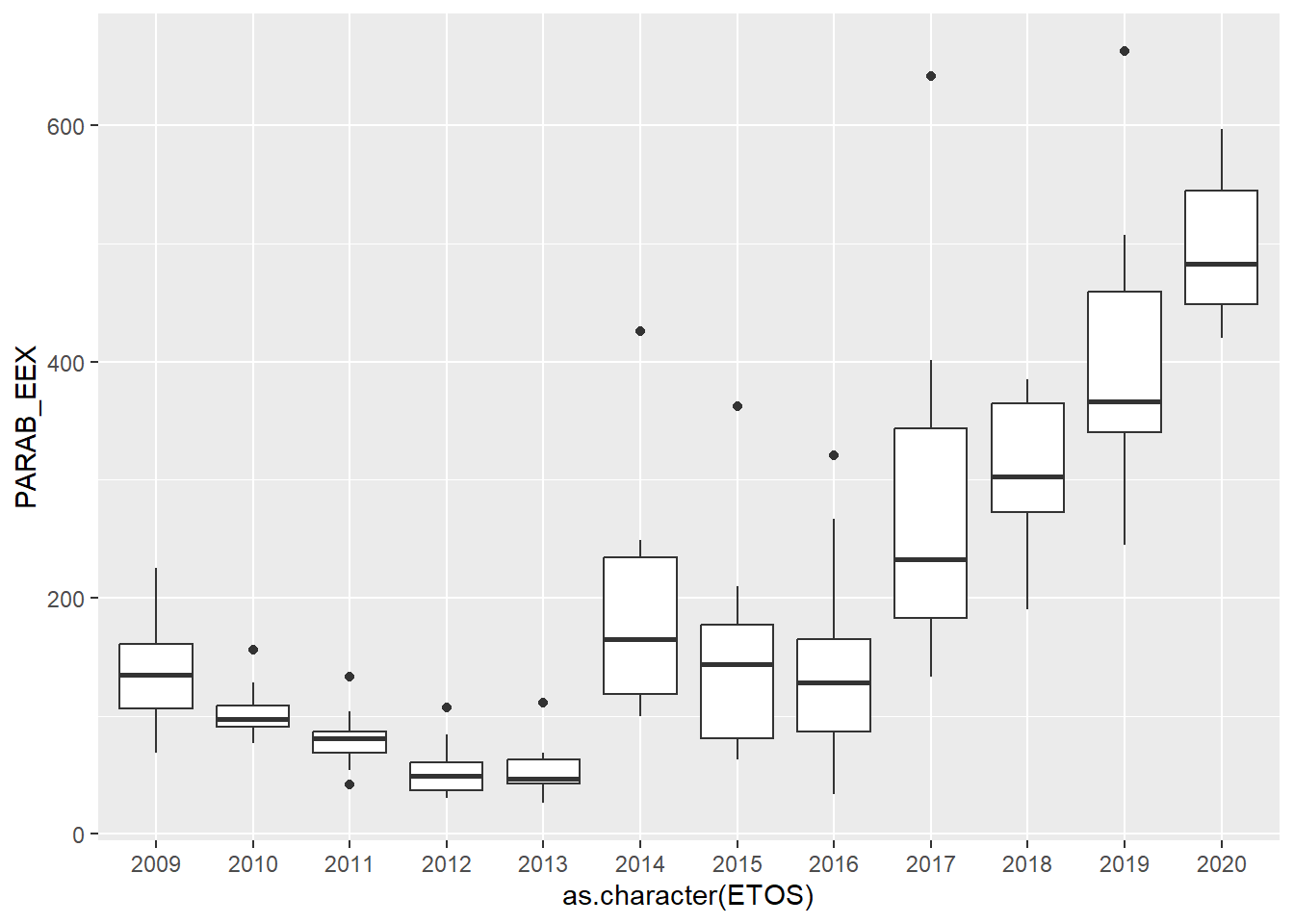

Φυσικά, αν θελήσουμε να υπάρχουν και σημεία συγχρόνως, γράφουμε:

ParabEEXboxEtos + geom_boxplot(outlier.shape = NA) + geom_jitter(shape=16, size=1,position=position_jitter(0.2))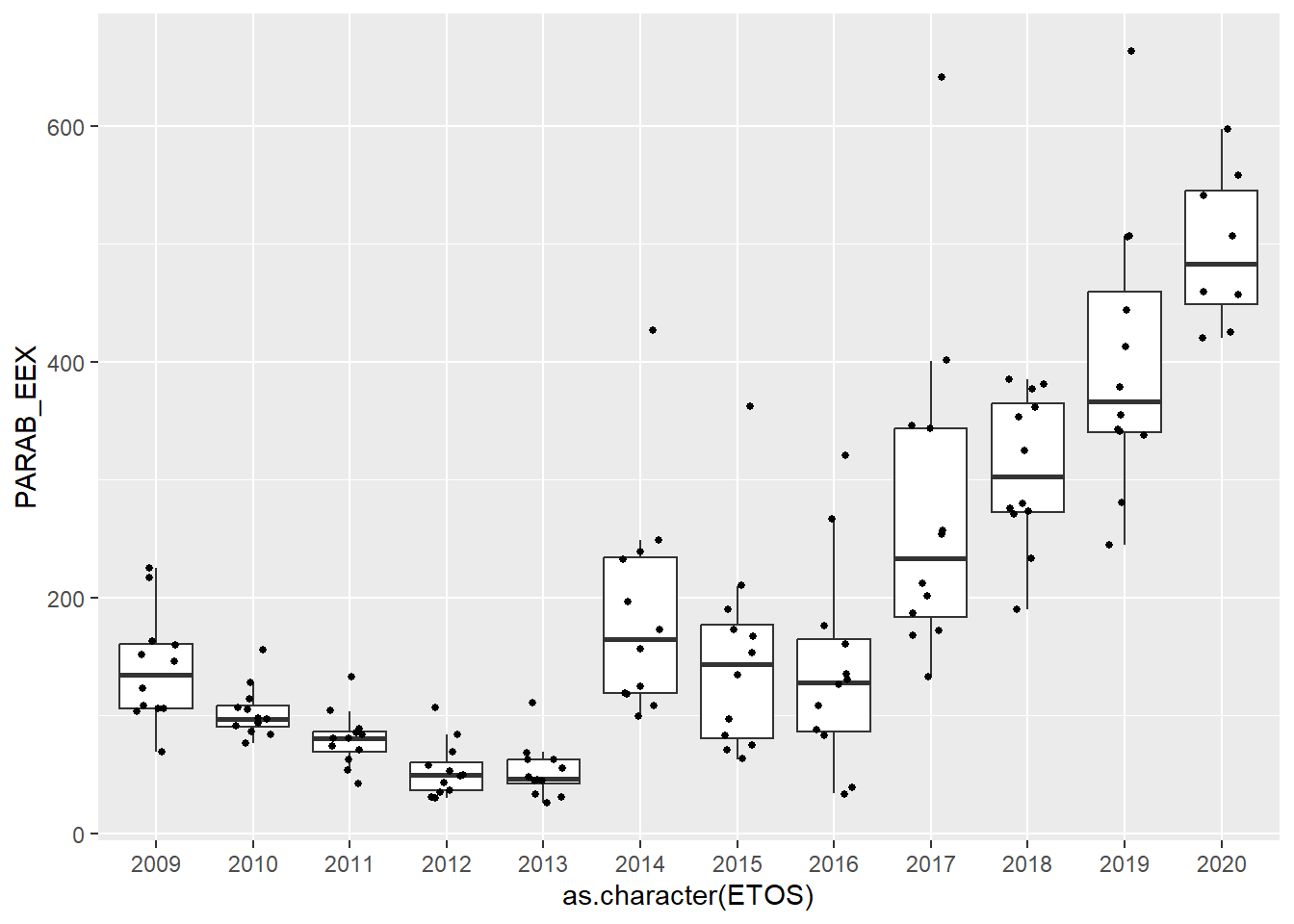

Πάνω στα τελευταία θηκογράμματα θα μπορούσαμε να κάναμε κάποιες αισθητικές παρεμβάσεις μέσω των επιλογών color= και fill=. Ας υποθέσουμε ότι φτιάχνουμε μια νέα σειρά από θηκογράμματα με βάση τις παραβιάσεις του κάθε μήνα. Αυτό θα γίνει γράφοντας αρχικά:

mines <- c("Ir","Fe","Mr","Ar","Ma","In","Il","Au","Se","Ok","No","De")

και ακολούθως:

ParabEEXboxMinas1 <- ggplot(enaerParab, aes(x=MHNAS, y=PARAB_EEX, color=MHNAS))
ParabEEXboxMinas1 + geom_boxplot() + xlim(mines)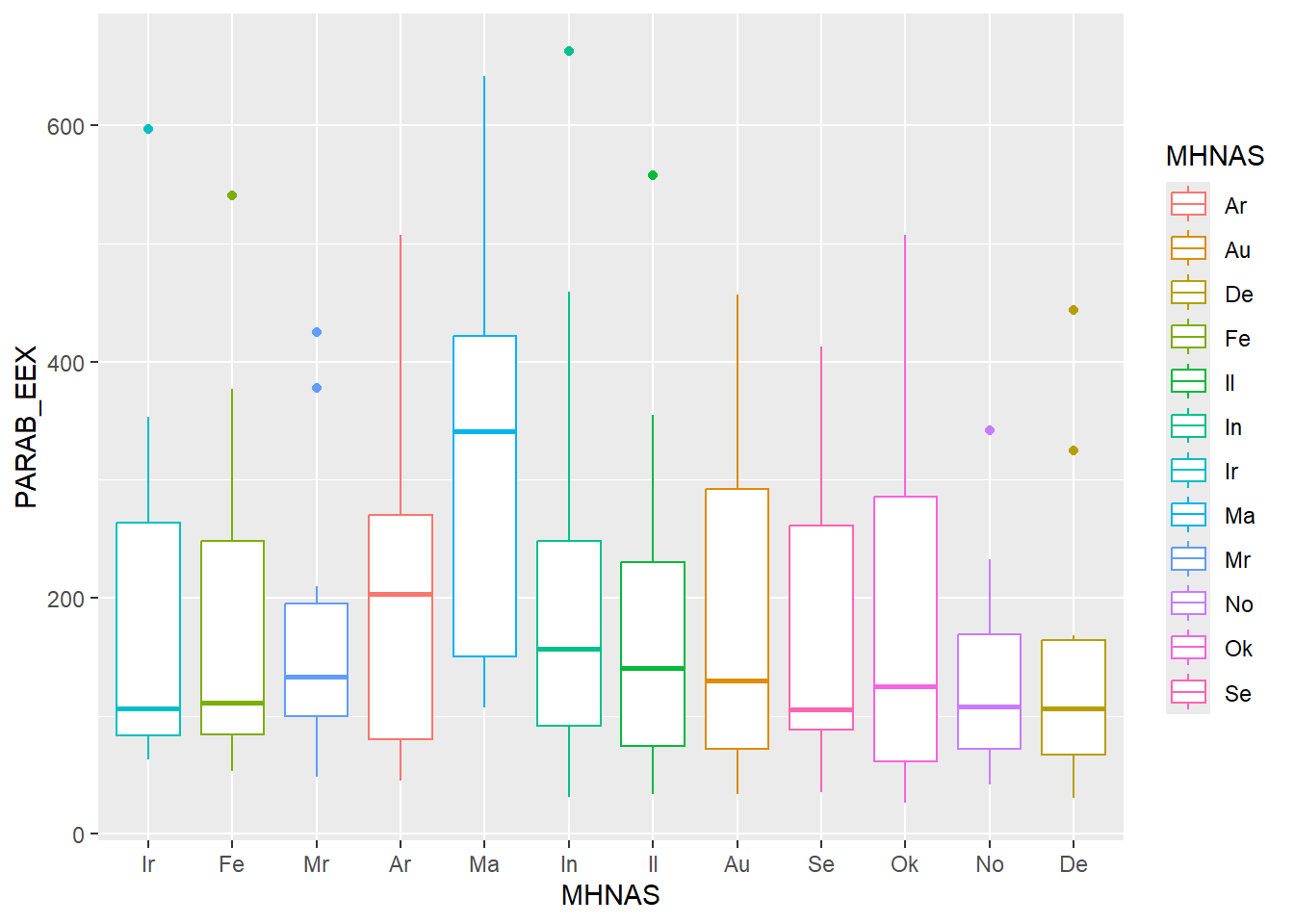

Όπου, φυσικά, η προσθήκη της xlim(mines) έγινε για να μπουν οι μήνες στη σωστή σειρά.

Αν τώρα θέλουμε να διαφοροποιούνται βάσει του χρώματος γεμίσματος, γράφουμε:

ParabEEXboxMinas2 <- ggplot(enaerParab, aes(x=MHNAS, y=PARAB_EEX, fill=MHNAS))
ParabEEXboxMinas2 + geom_boxplot() + xlim(mines)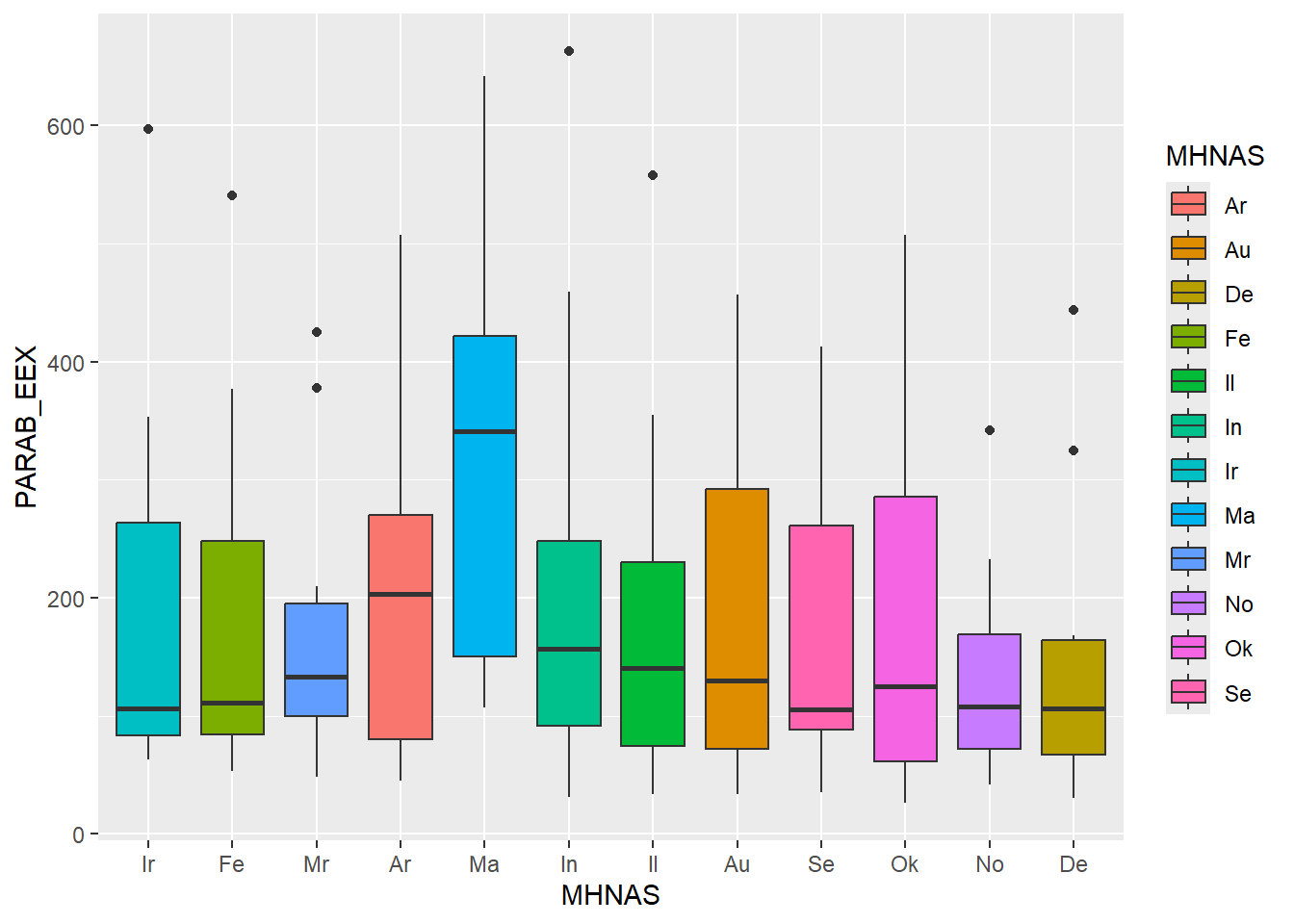

Ο κώδικας όλης αυτής της ενότητας είναι ο:

rm(list = ls())
mean(enaerParab$PARAB_EEX)
range(enaerParab$PARAB_EEX)
sd(enaerParab$PARAB_EEX)
sdPop <- function(x) sqrt(mean((x-mean(x))^ 2))
mean(enaerParab$PARAB_EEX)-3*sd(enaerParab$PARAB_EEX)
mean(enaerParab$PARAB_EEX)+3*sd(enaerParab$PARAB_EEX)
enaerParabApon <- enaerParab[enaerParab$PARAB_EEX>634.3057, ]
enaerParabApon
IQR(enaerParab$PARAB_EEX)
quantile(enaerParab$PARAB_EEX)
boxplot(enaerParab$PARAB_EEX)
boxplot(enaerParab$PARAB_EEX, horizontal=TRUE)
if(!require(ggplot2)){
    install.packages("ggplot2")
    library(ggplot2)
}
ParabEEXbox <- ggplot(enaerParab, aes(x="", y=PARAB_EEX))
ParabEEXbox + geom_boxplot()
ParabEEXbox + geom_boxplot() + coord_flip()
ParabEEXbox + geom_boxplot(outlier.shape = 0, outlier.size = 4)
ParabEEXbox + geom_boxplot() + geom_dotplot(binaxis='y', stackdir='center', dotsize=1)
ParabEEXbox + geom_boxplot() + geom_jitter(shape=16, size=1,position=position_jitter(0.2))
ParabEEXbox + geom_boxplot(outlier.shape = NA) + geom_jitter(shape=16, size=1,position=position_jitter(0.2))
ParabEEXboxEtos <- ggplot(enaerParab, aes(x=ETOS, y=PARAB_EEX))
ParabEEXboxEtos + geom_boxplot()
ParabEEXboxEtos <- ggplot(enaerParab, aes(x=as.character(ETOS), y=PARAB_EEX))
ParabEEXboxEtos + geom_boxplot()
ParabEEXboxEtos + geom_boxplot(outlier.shape = NA) + geom_jitter(shape=16, size=1,position=position_jitter(0.2))
mines <- c("Ir","Fe","Mr","Ar","Ma","In","Il","Au","Se","Ok","No","De")
ParabEEXboxMinas1 <- ggplot(enaerParab, aes(x=MHNAS, y=PARAB_EEX, color=MHNAS))
ParabEEXboxMinas1 + geom_boxplot() + xlim(mines)
ParabEEXboxMinas2 <- ggplot(enaerParab, aes(x=MHNAS, y=PARAB_EEX, fill=MHNAS))
ParabEEXboxMinas2 + geom_boxplot() + xlim(mines)